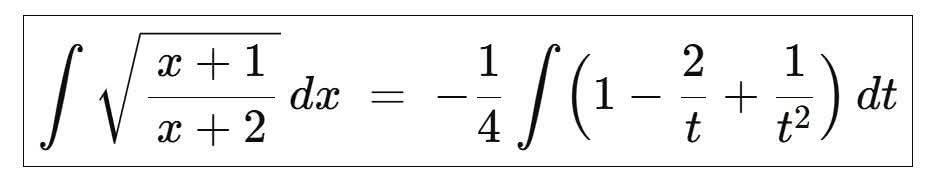Lmst

Никлаус Вирт и язык Pascal — легенды 80-х

В 1970 году молодой швейцарский учёный и программист Никлаус Вирт (Niklaus Wirth) выпустил первую версию Pascal. Прошло более полувека, автор умер в 89 лет, а вот Паскаль остаётся актуальным и популярным языком программирования.

https://habr.com/ru/companies/ruvds/articles/968706/

#Никлаус_Вирт #Pascal #Turbo_Pascal #Delphi #Niklaus_Wirth #Free_Pascal #Lazarus_IDE #Algol #Euler #ruvds_статьи

When a calculus student ends up solving this integral using partial fraction decomposition (PFD) or integration by parts (IBP), what they have actually done is successfully applied a classical algorithm. It’s like solving the Rubik’s cube by following an algorithm you found on the Internet: the heavy lifting of inventing PFD and IBP was done centuries ago by Bernoulli, Leibniz, and Gregory.

That said, the USM is, as far as I know, the only published general scheme that, for this kind of radical–rational integrals, systematically reduces the integrand to polynomial-type functions (Laurent polynomials, to be more precise). There’s no need to set up complicated PFDs or wrestle with sec³, which can be tricky with IBP. That’s what I call solving a problem, if you’ll allow me a bit of self-promotion.

You can find a first draft (I’ll soon upload a second version with benchmarks and some improvements) of the USM method on arXiv: https://arxiv.org/abs/2505.03754

#calculus #math #symmetrymatters #halfangleapproach #euler #integration

IBM đã cấp bằng sáng chế kỹ thuật toán 200 năm tuổi của Euler. Đây là một ví dụ về vấn đề sở hữu trí tuệ trong lĩnh vực toán học. #Euler #ToánHọc #SởHữuTríTuệ #IBM #Math #Patent

https://www.reddit.com/r/programming/comments/1ow61vh/ibm_patented_eulers_200_year_old_math_technique/

Gave a lecture today about Euler's theorem.
Then somehow it led to:
"There's a face, next muffin!"
Wondering what kind of vibe that sent out...

#teaching #graphtheory #euler

ah yes. #quaternions and #euler .
Of course. I should have known, right ?
:PopClutz:

( I wonder what #Euler would think if I used their lifework, to pose cute 3D Models to server for #Fanart :crazylaugh: )

#MikuMikuDance

@enigmatico would love this. As it involves loooooots of #math .

Método de Taylor

https://tubedu.org/w/2R99UjocyaoHnXWsqyZGnQ

Método de Euler

https://tubedu.org/w/pgFUPfobrHMEC6RS5bSBw5

🎩💡 Math sorcery alert! #RSA swapped Euler's math magic for Carmichael's card trick without even telling anyone! Who knew #encryption had a sense of humor? 🤷‍♂️🔒
https://www.johndcook.com/blog/2025/10/06/a-quiet-change-to-rsa/ #MathMagic #Humor #Carmichael #Euler #HackerNews #ngated

#nowplaying #bandcamp

The Dawn Identity
by The Abstract Observer

https://the-abstract-observer.bandcamp.com/album/the-dawn-identity

#music #ambient #piano #contemporary #electronic #euler #experimental #identity #imaginary #instrumental #irrational #math #minimalism #Antarctica

Played with the BEST theorem a little yesterday:

#math #besttheorem #eulerianCircuits #circuit #euler

a screenshot of a graph ABCD on graph paper with two arrows coming from and to node pairs AB, AC, BC, and CD. On the right is information for the BEST theorem showing the number of arborescences, product of (deg -1)! for nodes and the BEST calculation showing the number of eulerian circuits. The determinant math is shown as well with a note that the graph is eulerian because the number of in and out degrees is equal for all nodes. One spanning tree on the graph is highlighted with bold and there are buttons to go to the next. were are 3 in total given by the determinant/arborescences. There are teal tones in the background and on the nodes/vertices.

2/ Wusstet Ihr, dass #Euler die Planung der Trockenlegung des #Oderbruchs gemacht hat. Steht nicht in #Wikipedia, sollte es aber.

Ansonsten das Oderbruch ist wunderbar. Da kann man auch #Urlaub machen. Auf dem Deich Rad fahren usw.

#Mathematik

One day, one decomposition
A001838: Numbers k such that phi(k+2) = phi(k) + 2

3D graph, threejs - webGL ➡️ https://decompwlj.com/3Dgraph/A001838.html
3D graph Gen, threejs animation ➡️ https://decompwlj.com/3DgraphGen/A001838.html
2D graph, first 500 terms ➡️ https://decompwlj.com/2Dgraph500terms/A001838.html

#decompwlj #math #mathematics #sequence #OEIS #javascript #php #3D #numbers #phi #Euler #totient #function #graph #threejs #webGL

Decomposition into weight × level + jump of A001838 in 3D (threejs - WebGL) (log(weight), log(level), log(jump))

Decomposition into weight × level + jump of A001838 in 2D (log(weight), log(level))

One day, one decomposition
A001494: Numbers k such that phi(k) = phi(k+2)

3D graph, threejs - webGL ➡️ https://decompwlj.com/3Dgraph/A001494.html
3D graph Gen, threejs animation ➡️ https://decompwlj.com/3DgraphGen/A001494.html
2D graph, first 500 terms ➡️ https://decompwlj.com/2Dgraph500terms/A001494.html

#decompwlj #math #mathematics #sequence #OEIS #javascript #php #3D #numbers #Euler #totient #function #phi #graph #threejs #webGL

Decomposition into weight × level + jump of A001494 in 3D (threejs - WebGL) (log(weight), log(level), log(jump))

Decomposition into weight × level + jump of A001494 in 2D (log(weight), log(level))

"Euler calculated without any apparent effort, as men breathe, as eagles sustain themselves in the air." – François Arago (1786-1853)
#quote #mathematics #maths #math #Euler

Portrait of François Arago, and a quote : "Euler calculated without any apparent effort, as men breathe, as eagles sustain themselves in the air."

"Euler calculait sans aucun effort apparent, comme les hommes respirent, comme les aigles se soutiennent dans les airs." – François Arago (1786-1853)
#citation #mathématiques #maths #math #Euler

Portrait de François Arago, et une citation : "Euler calculait sans aucun effort apparent, comme les hommes respirent, comme les aigles se soutiennent dans les airs."

If, 14 years ago, you saw my Ignite lightning talk on #Euler’s identity and have been left hanging on the final “Gaussian Integral” slide - which I said was “a story for another day”…

#Numberphile have just done an amazing video on it, which is very enjoyable and I highly recommend.

https://youtu.be/WiO2Ku7V1rw?si=76uYfvxLkDQk59zg

(My original video: https://youtu.be/vHaPyuEkK4A?si=UHtkzFpjnUxDfdZ4)

Today's bugbear: Mathematicians who correct other people's pronunciation of Loenhard Euler's surname while completely mangling his first name.

#maths #math #euler

🤝 TAC (TON Application Chain) se asocia con #Curve, #Morpho y #Euler tras recaudar $11.5M para integrar #DeFi en Telegram. ¿Un nuevo impulso para la adopción masiva?

Of course this was known to many famous #mathematicians, like #Euler and #Jacobi and they solved the equations in terms of #EllipticIntegrals. I find it satisfying to be able to visualize the #dynamics of the this system, using #FreeSoftware, such as #WxMaxima.

USM really does slash the rote burden, chiefly because one handful of exponential/hyperbolic identities replaces a patchwork of separate trig, inverse-trig, radical and Euler recipes.

Article (draft): https://arxiv.org/abs/2505.03754

#math #calculus #integral #new #euler #arxiv #halfangleapproach #symmetrymatters

#Euler

Client Info