Continued from https://pixelfed.social/p/Splines/808187718454868394
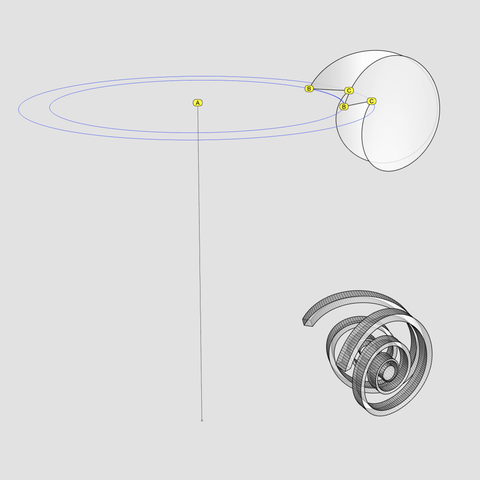
Explode the wedge on the top with curved faces and discard everything except the two faces.
Centered on the column axis marked with A, draw two concentric circles parallel to the XY plane — one with radius AB and another with radius AC. Split both circles with the two wedge faces.
Using the edges of the two wedge faces as #rails and using the two arcs BB and CC as #sweepingCurves, perform a #sweepTwoRails operation to generate a concave surface. Join this concave surface with the two faces.
The shape we just produced still has an open hole between the two arcs BB and CC. Cap this #planarHole to create an #airtight wedge shape with curved faces. As always, check for #nakedEdges and #nonManifoldEdges.
Align the wedge shape and the two 16 units thick spirals from the previous post. Then rotate both 45° about the column axis. Rotate and copy them again at 90° about the column axis until you have the curved volutes on all four corners.
#airtight
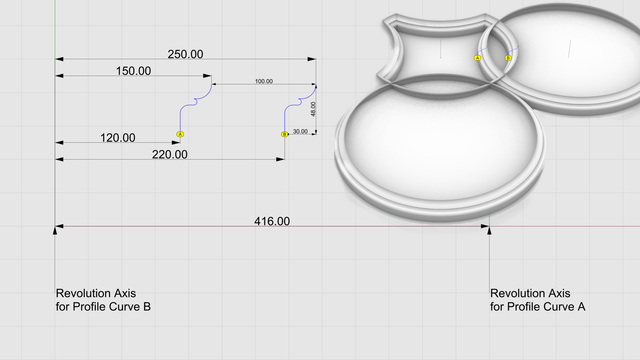
Left side of this diagram shows the #profileCurves for the cap of #ModernIonicCapital from the front. The right side shows a perspective view of the cap surfaces obtained by revolving the profile curves about their respective axes and after some of those have been trimmed away
The measurements for the floor plan of the modern ionic capital are given in https://pixelfed.social/p/Splines/807782440025967685 with further links to relevant pages in #Scarlata's book at the bottom.
I won't bore you with the bottom portion of the modern #capital because it is very similar to that of the classic capital shown in https://pixelfed.social/p/Splines/792124787573855518. A significant difference is that the bottom #ovolo is shorter, with a total height of 32 units instead of 40
For the cap, we need two identical copies of a single profile curve that is 30 units wide and 48 units tall. The curves marked by A and B in the diagram are oriented in the same direction and are spaced 100 units from each other.
The bottom of profile curve A lines up with the neck of the #columnShaft at 120 units from the column axis. The revolution axis for this curve is located at 416 units from the column axis at the center of the largest circle in the floor plan.
We #revolve profile curve A full circle about its revolution axis. Then, we #rotate the resulting surface about the column axis to get 4 identical copies.
We revolve profile curve B full circle about the column axis. Then, we trim the resulting surface along with the 4 others at each intersection to get the side and corner surfaces for the cap of the capital.
We #join the trimmed surfaces, cap #planarHoles to convert them into a closed solid, and verify that the resulting solid is #airtight with no #nakedEdges and no #nonManifoldEdges.
The cap is in the correct final orientation. The volutes will be at 45° angles, but when we construct them, it will be easier to rotate the whole plan 45° so that the #volute #spiral is on the XZ plane.
The measurements for the floor plan of the modern ionic capital are given in https://pixelfed.social/p/Splines/807782440025967685 with further links to relevant pages in #Scarlata's book at the bottom.
I won't bore you with the bottom portion of the modern #capital because it is very similar to that of the classic capital shown in https://pixelfed.social/p/Splines/792124787573855518. A significant difference is that the bottom #ovolo is shorter, with a total height of 32 units instead of 40
For the cap, we need two identical copies of a single profile curve that is 30 units wide and 48 units tall. The curves marked by A and B in the diagram are oriented in the same direction and are spaced 100 units from each other.
The bottom of profile curve A lines up with the neck of the #columnShaft at 120 units from the column axis. The revolution axis for this curve is located at 416 units from the column axis at the center of the largest circle in the floor plan.
We #revolve profile curve A full circle about its revolution axis. Then, we #rotate the resulting surface about the column axis to get 4 identical copies.
We revolve profile curve B full circle about the column axis. Then, we trim the resulting surface along with the 4 others at each intersection to get the side and corner surfaces for the cap of the capital.
We #join the trimmed surfaces, cap #planarHoles to convert them into a closed solid, and verify that the resulting solid is #airtight with no #nakedEdges and no #nonManifoldEdges.
The cap is in the correct final orientation. The volutes will be at 45° angles, but when we construct them, it will be easier to rotate the whole plan 45° so that the #volute #spiral is on the XZ plane.
#IonicColumn #Flutes
In https://pixelfed.social/p/Splines/799864068250003272 I mentioned rounding off the radius of the bottom circle, but you don't have to. #CAD tools are perfectly happy working with 15.0728 or even higher precision as they are with 15.
After placing the two circles as described in that post, use the full #primaryProfileCurve of the shaft from https://pixelfed.social/p/Splines/791794072490907090 as a #sweepingRail and the two circles for the flutes as the #sweepingCurves, and #sweepOneRail for the body of a single flute. Close #planarHoles on both ends to get an #airtight solid.
Then draw a sphere at the center of the top circle using the same radius as the circle, and perform a #booleanUnion between the sphere and the flute body.
If you want a round bottom for the flute, repeat the sphere at the center of the larger circle using the same radius (15.0 or 15.0728) and perform another boolean union to get one flute.
Switch to the top view and make 24 copies of the flute (including the original) centered at the column axis and #group the 24 flutes.
Finally, perform a #booleanDifference with the flutes group on a copy of the solid #unadornedShaft to get a fluted variant.
The result is a column shaft with flutes carved out. Save the flutes separately for future reuse.
This concludes the entire #IonicOrder, including all #decorativeElements.
Now we pause and reflect: The whole exercise seemed like one of #art and #sculpture. Where is the #architecture in all of this?
Without a ceiling or a roof, there is no building. Without additional columns or walls, there is no ceiling. So, while we have completed the Ionic Order itself, we only have the first #buildingBlock — a single column.
Next step is to repeat the columns to create a #colonnade, which together with supporting walls or additional colonnades can support a ceiling.
Just like with everything else in design, there are rules of proportion for #intercolumniation, or space between columns.
In https://pixelfed.social/p/Splines/799864068250003272 I mentioned rounding off the radius of the bottom circle, but you don't have to. #CAD tools are perfectly happy working with 15.0728 or even higher precision as they are with 15.
After placing the two circles as described in that post, use the full #primaryProfileCurve of the shaft from https://pixelfed.social/p/Splines/791794072490907090 as a #sweepingRail and the two circles for the flutes as the #sweepingCurves, and #sweepOneRail for the body of a single flute. Close #planarHoles on both ends to get an #airtight solid.
Then draw a sphere at the center of the top circle using the same radius as the circle, and perform a #booleanUnion between the sphere and the flute body.
If you want a round bottom for the flute, repeat the sphere at the center of the larger circle using the same radius (15.0 or 15.0728) and perform another boolean union to get one flute.
Switch to the top view and make 24 copies of the flute (including the original) centered at the column axis and #group the 24 flutes.
Finally, perform a #booleanDifference with the flutes group on a copy of the solid #unadornedShaft to get a fluted variant.
The result is a column shaft with flutes carved out. Save the flutes separately for future reuse.
This concludes the entire #IonicOrder, including all #decorativeElements.
Now we pause and reflect: The whole exercise seemed like one of #art and #sculpture. Where is the #architecture in all of this?
Without a ceiling or a roof, there is no building. Without additional columns or walls, there is no ceiling. So, while we have completed the Ionic Order itself, we only have the first #buildingBlock — a single column.
Next step is to repeat the columns to create a #colonnade, which together with supporting walls or additional colonnades can support a ceiling.
Just like with everything else in design, there are rules of proportion for #intercolumniation, or space between columns.
#Braids #3StrandBraids #MulticoloredBraids
To preserve the ability to print different strands in different colors when #3DPrinting, we must keep them separate. When #CNCMilling a block of wood or other material, we don't need to keep the strands separate.
To accommodate both kinds of output, I suggest that you keep the strands separate until the very end, and perform a #booleanUnion at the last possible stage after making a copy of the separate strands.
The topmost part of the diagram shows what the strands look like after a boolean union. Much of the internal structure is absorbed in the channel block, and overlapping parts of individual strands are eliminated.
The magenta curve from https://pixelfed.social/p/Splines/798252244743520392 is also shown here. Note that the location of the red cutting planes has changed slightly — Instead of 40 units from the origin, the first cutting plane is located at 39 because I ran into another limit that we must avoid.
Also, we need two blocks 120 units and 32 units long (not 24 units as was erroneously mentioned earlier). Turns out that cutting the strands at 32 units from the first cut puts us at 71 units from origin, and we run into another limit that destroys the #airtight properties of the cut solids. To get around that, we place the second cutting plane at 72 from origin to get a block 33 units long. The last cutting plane is at 159 units from origin, and when used with the first cutting plane it gives us a block 120 units long.
The lower portion of the diagram shows individual strands cut using the cutting planes as described above.
Depending on precision, you might or might not see a #nonmanifoldEdge on the second strand when cutting a length of 33 units. With precision set to 1/10 micron, which is ~100 times finer than current high-end #3DPrinters, I got a non-manifold edge.
Sometimes the fix is easy — Just #explode the solid, and rejoin the tiny surface fragments. Experiment with different precision settings.
To preserve the ability to print different strands in different colors when #3DPrinting, we must keep them separate. When #CNCMilling a block of wood or other material, we don't need to keep the strands separate.
To accommodate both kinds of output, I suggest that you keep the strands separate until the very end, and perform a #booleanUnion at the last possible stage after making a copy of the separate strands.
The topmost part of the diagram shows what the strands look like after a boolean union. Much of the internal structure is absorbed in the channel block, and overlapping parts of individual strands are eliminated.
The magenta curve from https://pixelfed.social/p/Splines/798252244743520392 is also shown here. Note that the location of the red cutting planes has changed slightly — Instead of 40 units from the origin, the first cutting plane is located at 39 because I ran into another limit that we must avoid.
Also, we need two blocks 120 units and 32 units long (not 24 units as was erroneously mentioned earlier). Turns out that cutting the strands at 32 units from the first cut puts us at 71 units from origin, and we run into another limit that destroys the #airtight properties of the cut solids. To get around that, we place the second cutting plane at 72 from origin to get a block 33 units long. The last cutting plane is at 159 units from origin, and when used with the first cutting plane it gives us a block 120 units long.
The lower portion of the diagram shows individual strands cut using the cutting planes as described above.
Depending on precision, you might or might not see a #nonmanifoldEdge on the second strand when cutting a length of 33 units. With precision set to 1/10 micron, which is ~100 times finer than current high-end #3DPrinters, I got a non-manifold edge.
Sometimes the fix is easy — Just #explode the solid, and rejoin the tiny surface fragments. Experiment with different precision settings.
#Braids #3StrandBraids
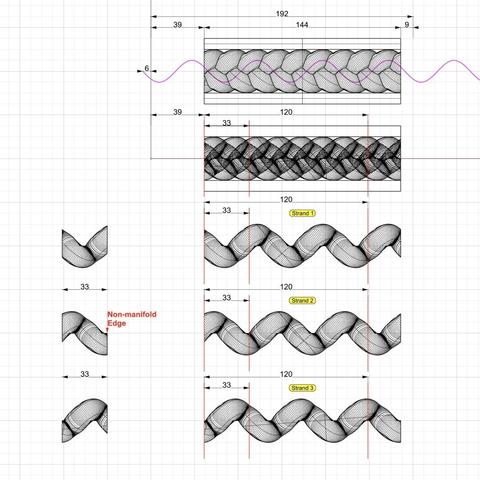
From the #profileCurve in https://pixelfed.social/p/Splines/798252244743520392, extrude a 192 units long solid starting at the origin.
Copy the original strand twice and place the copies 16 and 32 units to the right of the original. The three strands are shown here in orange, white, and green. Because of these shifts, the starting and ending portions of the braid are not usable. So use #cuttingSurfaces 40 units from the origin and 184 units from the origin. This will give you a clean 3-strand braid 144 units long.
For the #capital, we need two sections, one that is 120 units long and another that is 24 units long. So be prepared to split the braid-channel assembly one more time, but not yet.
Before making further cuts, make a copy of the entire 144 units-long braid assembly and save it separately. Then perform a #nonuniformScale with origin as the base point, and scale only in Z to shrink the height of channel from 12 to 6. The entire assembly will now have a height of 8.1 units down from 16.2. The nonuniformly-scaled version is not shown here.
The image on the top-right shows a rectangular profile curve sweeping the same rail curve as before, giving it sharp corners.
The image on bottom-left shows a profile curve derived from sections of the rail curve itself that were cut, rotated, and reflected to form a closed non-planar outline. When we sweep this closed curve on the original rail, we get smooth top and bottom surfaces and sharp edges on the sides.. After you sweep this shape, you will find that the ends are still open.
There is no way to close the holes with what we have discussed so far because the edges are not planar. To fix this, you will have to create #patchSurfaces using the edge curves of the profile on both ends and join all three surfaces. Check for #nakedEdges and #nonManifoldEdges for #airtight fit.
The last image shows a 5-point star with sharp angular lines swept on the same rail curve.
From the #profileCurve in https://pixelfed.social/p/Splines/798252244743520392, extrude a 192 units long solid starting at the origin.
Copy the original strand twice and place the copies 16 and 32 units to the right of the original. The three strands are shown here in orange, white, and green. Because of these shifts, the starting and ending portions of the braid are not usable. So use #cuttingSurfaces 40 units from the origin and 184 units from the origin. This will give you a clean 3-strand braid 144 units long.
For the #capital, we need two sections, one that is 120 units long and another that is 24 units long. So be prepared to split the braid-channel assembly one more time, but not yet.
Before making further cuts, make a copy of the entire 144 units-long braid assembly and save it separately. Then perform a #nonuniformScale with origin as the base point, and scale only in Z to shrink the height of channel from 12 to 6. The entire assembly will now have a height of 8.1 units down from 16.2. The nonuniformly-scaled version is not shown here.
The image on the top-right shows a rectangular profile curve sweeping the same rail curve as before, giving it sharp corners.
The image on bottom-left shows a profile curve derived from sections of the rail curve itself that were cut, rotated, and reflected to form a closed non-planar outline. When we sweep this closed curve on the original rail, we get smooth top and bottom surfaces and sharp edges on the sides.. After you sweep this shape, you will find that the ends are still open.
There is no way to close the holes with what we have discussed so far because the edges are not planar. To fix this, you will have to create #patchSurfaces using the edge curves of the profile on both ends and join all three surfaces. Check for #nakedEdges and #nonManifoldEdges for #airtight fit.
The last image shows a 5-point star with sharp angular lines swept on the same rail curve.
#Braids #3StrandBraids
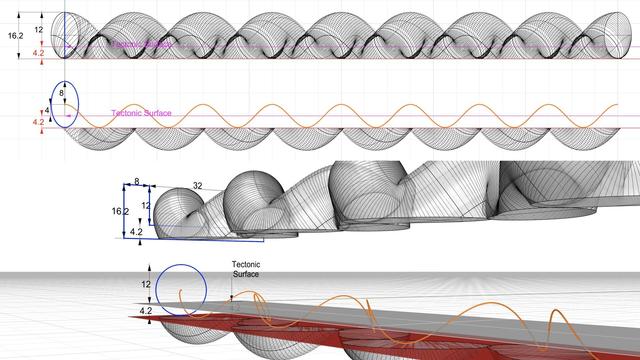
After we #sweepOneRail with the blue #sweepingCurve on the orange #railCurve for the #braid strand, we cap #planarHoles to get a single #airtight strand.
As described in https://pixelfed.social/p/Splines/798015349727305297, the radius of the blue circle is 8 units, and the total height of a strand swept by that circle is 24 units. Half of that is above the #tectonic surface, which is still twice of what #Vignola documented in #RegolaArchitettura.
We will apply #nonuniformScaling in the Z direction to reduce the height in half while keeping the length (X) and width (Y) the same. But before we do that we split and discard some of the bottom portion of the strand that is below the tectonic surface and is not needed.
The top half of the figure shows the front view of a single strand. The bottom shows the perspective view of the same strand.
Note that the orange braid rail starts at the center of the blue sweeping circle which looks like an ellipse in the front view. The orange rail itself looks like a flat sinusoid in the front view, but its beautiful meandering shape is really apparent in the perspective view.
The orange rail curve is centered on the "ground" or XY plane, which is also where the #tectonicSurface for the braid is. The amplitude of the orange curve (maximum or minimum from axis of the curve) is 4 units. We need to preserve the geometry of the strand at least up to the bottom of the orange rail.
If we split the strand exactly at 4 units below the ground plane, we hit a limit that not all #CAD tools are able to handle. To get around, we extend it past that limit by an arbitrarily small fraction, like 0.2, and discard the portions below. We could have extended it by 0.1 or 0.3 but it wouldn't have mattered.
Next, we draw a profile curve for the braid channel which is 32 units wide and its groove is 12 units tall for now. The rims on both sides of the channel are each 8 units wide. Total height of rim and channel is 16.2 units
After we #sweepOneRail with the blue #sweepingCurve on the orange #railCurve for the #braid strand, we cap #planarHoles to get a single #airtight strand.
As described in https://pixelfed.social/p/Splines/798015349727305297, the radius of the blue circle is 8 units, and the total height of a strand swept by that circle is 24 units. Half of that is above the #tectonic surface, which is still twice of what #Vignola documented in #RegolaArchitettura.
We will apply #nonuniformScaling in the Z direction to reduce the height in half while keeping the length (X) and width (Y) the same. But before we do that we split and discard some of the bottom portion of the strand that is below the tectonic surface and is not needed.
The top half of the figure shows the front view of a single strand. The bottom shows the perspective view of the same strand.
Note that the orange braid rail starts at the center of the blue sweeping circle which looks like an ellipse in the front view. The orange rail itself looks like a flat sinusoid in the front view, but its beautiful meandering shape is really apparent in the perspective view.
The orange rail curve is centered on the "ground" or XY plane, which is also where the #tectonicSurface for the braid is. The amplitude of the orange curve (maximum or minimum from axis of the curve) is 4 units. We need to preserve the geometry of the strand at least up to the bottom of the orange rail.
If we split the strand exactly at 4 units below the ground plane, we hit a limit that not all #CAD tools are able to handle. To get around, we extend it past that limit by an arbitrarily small fraction, like 0.2, and discard the portions below. We could have extended it by 0.1 or 0.3 but it wouldn't have mattered.
Next, we draw a profile curve for the braid channel which is 32 units wide and its groove is 12 units tall for now. The rims on both sides of the channel are each 8 units wide. Total height of rim and channel is 16.2 units
#Braids #3StrandBraids
With the #rail curve for a #braid strand in https://pixelfed.social/p/Splines/797916882329430160, we can start the construction of a braid that matches the sketch in #Vignola's #RegolaArchitettura shown in https://pixelfed.social/p/Splines/793215298082967733.
The strands for this braid have a radius of 1 part or 8 units. So their diameter is 16 units, and the braid itself is 32 units wide.
To create one strand, we start with a circle of radius of 8 units perpendicular to the tip of the orange curve. We use the orange curve as a #railCurve and the blue circle as the #sweepingCurve in the #sweepOneRail operation.
Note that the circle appears distorted like an oval in all views — front view is on top-left, top view on top-right, right view in bottom-left, and perspective view in bottom-right. That is because the circle is perpendicular to the rail curve, not to any of the "world" coordinate planes. If the sweeping curve does not appear like an angled line in the top view, something is wrong.
After the sweep, close #planarHoles to get a solid strand and, as always, check for #nakedEdges and #nonManifoldEdges to ensure an #airtight object.
Refer again to the middle portion of the top diagram in https://pixelfed.social/p/Splines/793215298082967733 between the two bell shapes of the scrolls. The total width of the #tectonic surface on which the braid will be laid is 4 parts or 32 units wide. The braid has a rim 8 units wide on both sides that rises 6 units above the tectonic surface. Half of the braid should be above the tectonic surface, meaning that the total height of the braid should be 12 units.
If you check the bounding box of this strand, you find that it is indeed 32 units wide as needed, but the height is 24 units. So we have to apply #nonuniformScaling to keep X and Y scale intact but halve the scale in the Z direction. This will reduce the roundness of the strand and cut its height in half to 12 as needed.
With the #rail curve for a #braid strand in https://pixelfed.social/p/Splines/797916882329430160, we can start the construction of a braid that matches the sketch in #Vignola's #RegolaArchitettura shown in https://pixelfed.social/p/Splines/793215298082967733.
The strands for this braid have a radius of 1 part or 8 units. So their diameter is 16 units, and the braid itself is 32 units wide.
To create one strand, we start with a circle of radius of 8 units perpendicular to the tip of the orange curve. We use the orange curve as a #railCurve and the blue circle as the #sweepingCurve in the #sweepOneRail operation.
Note that the circle appears distorted like an oval in all views — front view is on top-left, top view on top-right, right view in bottom-left, and perspective view in bottom-right. That is because the circle is perpendicular to the rail curve, not to any of the "world" coordinate planes. If the sweeping curve does not appear like an angled line in the top view, something is wrong.
After the sweep, close #planarHoles to get a solid strand and, as always, check for #nakedEdges and #nonManifoldEdges to ensure an #airtight object.
Refer again to the middle portion of the top diagram in https://pixelfed.social/p/Splines/793215298082967733 between the two bell shapes of the scrolls. The total width of the #tectonic surface on which the braid will be laid is 4 parts or 32 units wide. The braid has a rim 8 units wide on both sides that rises 6 units above the tectonic surface. Half of the braid should be above the tectonic surface, meaning that the total height of the braid should be 12 units.
If you check the bounding box of this strand, you find that it is indeed 32 units wide as needed, but the height is 24 units. So we have to apply #nonuniformScaling to keep X and Y scale intact but halve the scale in the Z direction. This will reduce the roundness of the strand and cut its height in half to 12 as needed.
#Braids #3StrandBraids
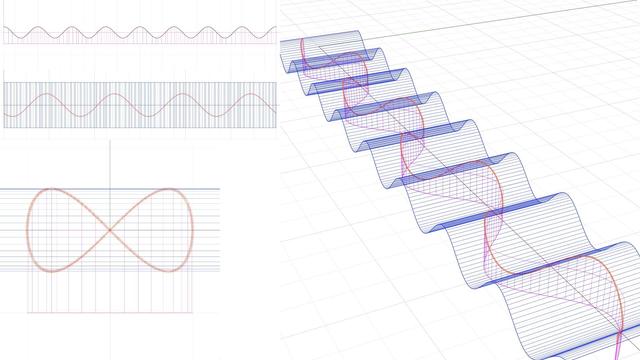
We are finally ready to convert the two #sinusoids from https://pixelfed.social/p/Splines/797893262102038801 into a single 3D curve that captures the essential geometry of a #braid strand.
First extrude the blue sinusoid into a surface that extends past the magenta sinusoid on both sides. Then draw a bounding box around the blue extrusion and trim the magenta sinusoid that falls outside the bounding box.
Discard the bounding box, and extrude the trimmed magenta sinusoid into a surface that extends past the blue extrusion on both sides.
Then split either surface with the other. It doesn't matter which surface is split and which is used as a cutting surface. The braid strand lies literally at the intersection of both surfaces.
I trimmed the magenta surface with the blue one and deleted the top portion to reveal the curve at the intersection — shown here in orange. In perspective view this curve continuously swerves from left to right and simultaneously from top to bottom as it progresses along the X axis.
This single curve has the characteristics of both sinusoids as seen in front and top views. In the side view, this looks like the #infinity symbol. So we have progressed from zero (with #helix), to plus (with #sinusoid), to infinity (with intersection of two #sinusoidal surfaces).
Once we have this curve, we can sweep a circle around it to make a round strand. We can change the radius of the circle to make thinner or thicker strands. We can slant the circles to give a "calligraphic" look to the strands. We can use ovals, rectangles, squares, stars, or any closed shape to give different surface properties to the strands — the possibilities are endless.
Once you have a closed #airtight strand with capped #planarHoles, make 2 more copies of the same strand. Shift the first copy by 1/3 the wavelength of the magenta sinusoid (48/3 = 16 units) and shift the second copy by 2/3 (48*2/3 = 32 units) while leaving the original one in its place.
We are finally ready to convert the two #sinusoids from https://pixelfed.social/p/Splines/797893262102038801 into a single 3D curve that captures the essential geometry of a #braid strand.
First extrude the blue sinusoid into a surface that extends past the magenta sinusoid on both sides. Then draw a bounding box around the blue extrusion and trim the magenta sinusoid that falls outside the bounding box.
Discard the bounding box, and extrude the trimmed magenta sinusoid into a surface that extends past the blue extrusion on both sides.
Then split either surface with the other. It doesn't matter which surface is split and which is used as a cutting surface. The braid strand lies literally at the intersection of both surfaces.
I trimmed the magenta surface with the blue one and deleted the top portion to reveal the curve at the intersection — shown here in orange. In perspective view this curve continuously swerves from left to right and simultaneously from top to bottom as it progresses along the X axis.
This single curve has the characteristics of both sinusoids as seen in front and top views. In the side view, this looks like the #infinity symbol. So we have progressed from zero (with #helix), to plus (with #sinusoid), to infinity (with intersection of two #sinusoidal surfaces).
Once we have this curve, we can sweep a circle around it to make a round strand. We can change the radius of the circle to make thinner or thicker strands. We can slant the circles to give a "calligraphic" look to the strands. We can use ovals, rectangles, squares, stars, or any closed shape to give different surface properties to the strands — the possibilities are endless.
Once you have a closed #airtight strand with capped #planarHoles, make 2 more copies of the same strand. Shift the first copy by 1/3 the wavelength of the magenta sinusoid (48/3 = 16 units) and shift the second copy by 2/3 (48*2/3 = 32 units) while leaving the original one in its place.
#EggsAndDarts continuation from https://pixelfed.social/p/Splines/796961505955555432
The slab height depends on the roundness of the egg and whether we have a concave design or not. If we are using a concave base, then top half of the egg is eliminated. For a fully round egg, that means the concave variant must scoop out up to 16 units deep. The dart slab will match the egg slab in depth.
To create the 3-dimensional shape of the dart, first #rotate the fin profile 90° in 3D space along the straight line at the bottom of the fin so that the rotated profile is perpendicular to the two #sweepRails for the dart.
Using the two sweep rails and the perpendicular fin profile, #sweepTwoRails to develop the surface of the dart. Remember to close the planar hole at the end of the fin to get a solid #airtight object. As always, check for #nakedEdges and #nonmanifoldEdges to stave off problems later.
#Extrude the bottom of the dart until it is flush with the bottom of the oval slab.
Two details worth noting in the dart design are:
1. The most exaggerated portions of the dart fin are sliced off when the eggs are sliced. After slicing, the size of the fin is roughly in proportion to the rims of the eggs on both sides.
2. There is a gap between the dart arrow and the oval slab. See the gap between points R and T in https://pixelfed.social/p/Splines/796961505955555432. This gap is necessary and will automatically close when we transfer the egg and dart to the #doublyCurved surface of the #ovolo on the #capital of the #IonicColumn. That is because the Ovolo is shaped like a bowl whose top has a bigger radius than the bottom. As a result, the motif will be warped, and its bottom will be condensed to fit the smaller radius at the bottom, closing the gap in the process.
If you plan to use the eggs and darts motif on a linear surface where there is no warping, experiment with the arrow and tip for a pleasing result.
The slab height depends on the roundness of the egg and whether we have a concave design or not. If we are using a concave base, then top half of the egg is eliminated. For a fully round egg, that means the concave variant must scoop out up to 16 units deep. The dart slab will match the egg slab in depth.
To create the 3-dimensional shape of the dart, first #rotate the fin profile 90° in 3D space along the straight line at the bottom of the fin so that the rotated profile is perpendicular to the two #sweepRails for the dart.
Using the two sweep rails and the perpendicular fin profile, #sweepTwoRails to develop the surface of the dart. Remember to close the planar hole at the end of the fin to get a solid #airtight object. As always, check for #nakedEdges and #nonmanifoldEdges to stave off problems later.
#Extrude the bottom of the dart until it is flush with the bottom of the oval slab.
Two details worth noting in the dart design are:
1. The most exaggerated portions of the dart fin are sliced off when the eggs are sliced. After slicing, the size of the fin is roughly in proportion to the rims of the eggs on both sides.
2. There is a gap between the dart arrow and the oval slab. See the gap between points R and T in https://pixelfed.social/p/Splines/796961505955555432. This gap is necessary and will automatically close when we transfer the egg and dart to the #doublyCurved surface of the #ovolo on the #capital of the #IonicColumn. That is because the Ovolo is shaped like a bowl whose top has a bigger radius than the bottom. As a result, the motif will be warped, and its bottom will be condensed to fit the smaller radius at the bottom, closing the gap in the process.
If you plan to use the eggs and darts motif on a linear surface where there is no warping, experiment with the arrow and tip for a pleasing result.
After ensuring that the object in https://pixelfed.social/p/Splines/795271266191779399 is #airtight, extrude the front and rear planar surfaces by 1 part (8 units) on each end.
At the end of this step, you should have a solid #scroll object with a smooth surface except for the flat parts that will butt against the head of the unadorned #capital.
We have now concluded the #tectonic portions of the entire #IonicOrder. All that remains are decorative #eggsAndDarts that go on the #ovolo of the capital and the #3StrandBraid that goes on the scroll.
At the end of this step, you should have a solid #scroll object with a smooth surface except for the flat parts that will butt against the head of the unadorned #capital.
We have now concluded the #tectonic portions of the entire #IonicOrder. All that remains are decorative #eggsAndDarts that go on the #ovolo of the capital and the #3StrandBraid that goes on the scroll.
To create an #airtight solid object from the smooth surface in https://pixelfed.social/p/Splines/794868875707070193 that is suitable for #integration in the classic #IonicCapital, we need to trim the surface at specific points.
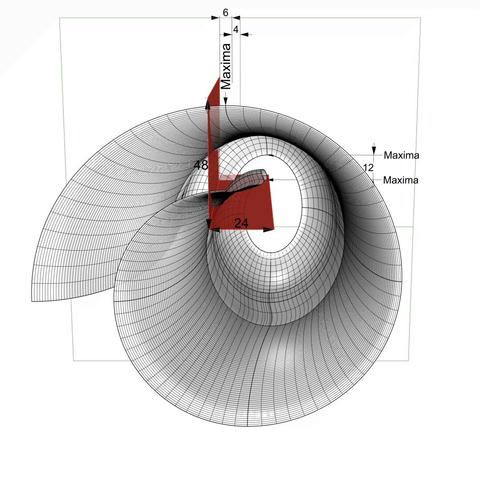
First draw an L shape that is 3 parts (24 units) wide and 6 parts (48 units) tall. The base of the L should align with the maxima of the last arc of the rear #spiral. The stem of the L should be 3/4 part (6 units) to the left of the maxima for the first arc of the front spiral, or 10 units to the left of the eye of the spiral.
#Extrude the L-shaped curve to create an L-shaped #cuttingSurface (shown here in red) that extends past both the front and the rear of the scroll surface.
Make a copy of the scroll surface so that you don't destroy the full original surface. Then, split the copy of the scroll surface with the cutting surface.
From the outside portion of the scroll surface, discard the portion to the left of the cutting surface, From the inside portion of the scroll surface, discard the portion immediately above the base of the cutting surface.
Save a copy of the cutting surface in case you need to repeat these steps, because in the next step we will carve out a portion of the cutting surface itself and join the flat faces of that carved out shape with the trimmed scroll surface.
First draw an L shape that is 3 parts (24 units) wide and 6 parts (48 units) tall. The base of the L should align with the maxima of the last arc of the rear #spiral. The stem of the L should be 3/4 part (6 units) to the left of the maxima for the first arc of the front spiral, or 10 units to the left of the eye of the spiral.
#Extrude the L-shaped curve to create an L-shaped #cuttingSurface (shown here in red) that extends past both the front and the rear of the scroll surface.
Make a copy of the scroll surface so that you don't destroy the full original surface. Then, split the copy of the scroll surface with the cutting surface.
From the outside portion of the scroll surface, discard the portion to the left of the cutting surface, From the inside portion of the scroll surface, discard the portion immediately above the base of the cutting surface.
Save a copy of the cutting surface in case you need to repeat these steps, because in the next step we will carve out a portion of the cutting surface itself and join the flat faces of that carved out shape with the trimmed scroll surface.
Compare the image here with that in https://pixelfed.social/p/Splines/794551798960473148 for smoothness.
When we discard the bands immediately adjacent to the front and rear bands (one between K and P and the other between Q and L in https://pixelfed.social/p/Splines/794105734853818690), we are left with three bands. The front band is 36 units deep the middle band between the frames marked P and Q is 25 units deep, and the rear band is 18 units deep.
We then split the middle band into two — a band 18 units deep adjacent to P and a band 7 units deep adjacent to Q.
Finally, we perform a #surfaceBlend between the front band and the narrower split band while maintaining tangency. This produces a new band that is 32 units deep. We perform another surface blend between the rear band and the wider split band maintaining tangency. This produces a new band that is 14 units deep. We then discard the two bands that we had split from the original middle band.
The end result is 4 bands total — A front band that is 36 units deep, a blended band 32 units deep adjacent to the front band, a blended band 14 units deep adjacent to the rear band, and the rear band that is 18 units deep.
When we join these 4 bands, we get the full #scroll surface that is 100 units deep. The final surface is smooth, and there is no hint of banding, as seen in this image with a polished gold #environmentMap.
This is the smooth surface whose back view is shown with a #zebraPattern in my introductory post at https://pixelfed.social/p/Splines/789956327130679640 and again in https://pixelfed.social/p/Splines/792828550887335575.
We were finally able to coax the scroll surface not just to "hug" the #modulatingSpirals, but also to stretch tightly and smoothly.
We have come a long way, but there's still more work to do. What we have right now is an open surface. We need to convert this into an #airtight closed object that we can use for #3DPrinting or #CNCMilling. We will do that in the next posts.
When we discard the bands immediately adjacent to the front and rear bands (one between K and P and the other between Q and L in https://pixelfed.social/p/Splines/794105734853818690), we are left with three bands. The front band is 36 units deep the middle band between the frames marked P and Q is 25 units deep, and the rear band is 18 units deep.
We then split the middle band into two — a band 18 units deep adjacent to P and a band 7 units deep adjacent to Q.
Finally, we perform a #surfaceBlend between the front band and the narrower split band while maintaining tangency. This produces a new band that is 32 units deep. We perform another surface blend between the rear band and the wider split band maintaining tangency. This produces a new band that is 14 units deep. We then discard the two bands that we had split from the original middle band.
The end result is 4 bands total — A front band that is 36 units deep, a blended band 32 units deep adjacent to the front band, a blended band 14 units deep adjacent to the rear band, and the rear band that is 18 units deep.
When we join these 4 bands, we get the full #scroll surface that is 100 units deep. The final surface is smooth, and there is no hint of banding, as seen in this image with a polished gold #environmentMap.
This is the smooth surface whose back view is shown with a #zebraPattern in my introductory post at https://pixelfed.social/p/Splines/789956327130679640 and again in https://pixelfed.social/p/Splines/792828550887335575.
We were finally able to coax the scroll surface not just to "hug" the #modulatingSpirals, but also to stretch tightly and smoothly.
We have come a long way, but there's still more work to do. What we have right now is an open surface. We need to convert this into an #airtight closed object that we can use for #3DPrinting or #CNCMilling. We will do that in the next posts.
From https://pixelfed.social/p/Splines/790645054230337543, we now have an open surface for the #IonicPedestal. To finish this, close the #planarHoles at the top and bottom with flat caps and join everything. And just like that, we have finished 1/3 of the complete #IonicOrder with very little work.
To ensure that your finished object is amenable to #3DPrinting or #CNCMilling, always check the edges of your object after all surfaces have been joined. Do this EVERY time you join surfaces to create a closed object.
Most CAD programs will offer edge analysis tools that let you detect #nakedEdges or #nonManifoldEdges. If you have either of those, your object is not #airtight, and you will not be able to physically realize it.
This version of the pedestal uses the classic variation of #CymaRecta and #CymaReversa. If you want to remain faithful to the original, then you are done.
However, designs are rarely static and they continue to evolve. There is an opportunity for a slight refinement at the top and bottom of the pedestal without compromising the integrity of the order, but it requires the introduction of a new kind of curve — a #helix, which is a coil-shaped 3D curve.
I will discuss the #helixVariation later. For now, look closely at the #basement and notice how pronounced the turns of the cyma recta are. Instead of using elliptical arcs in the #primaryProfileCurves of the cyma recta and cyma reversa, it is possible to substitute a half-turn of a helix that has been flattened to a 2D shape. The result is a softer, more gradual profile curve that produces a very refined shape.
To ensure that your finished object is amenable to #3DPrinting or #CNCMilling, always check the edges of your object after all surfaces have been joined. Do this EVERY time you join surfaces to create a closed object.
Most CAD programs will offer edge analysis tools that let you detect #nakedEdges or #nonManifoldEdges. If you have either of those, your object is not #airtight, and you will not be able to physically realize it.
This version of the pedestal uses the classic variation of #CymaRecta and #CymaReversa. If you want to remain faithful to the original, then you are done.
However, designs are rarely static and they continue to evolve. There is an opportunity for a slight refinement at the top and bottom of the pedestal without compromising the integrity of the order, but it requires the introduction of a new kind of curve — a #helix, which is a coil-shaped 3D curve.
I will discuss the #helixVariation later. For now, look closely at the #basement and notice how pronounced the turns of the cyma recta are. Instead of using elliptical arcs in the #primaryProfileCurves of the cyma recta and cyma reversa, it is possible to substitute a half-turn of a helix that has been flattened to a 2D shape. The result is a softer, more gradual profile curve that produces a very refined shape.
Client Info
Server: https://mastodon.social
Version: 2025.07
Repository: https://github.com/cyevgeniy/lmst