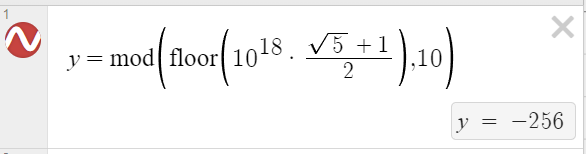1. IEEE standard 754 (floating point number arithmetic) which Desmos uses cannot accurately mod \(10\) at this high of a number (\(10^{18}\varphi \)), as when it tries to divide the large number by \(10\) and find the remainder, the last bits is \(512\) and \(2048\), and when getting divided by \(10\), these become \(256\) and \(512\) (with the precision). The mod algorithm accidentally grabs the \(256\) bit and reverses the sign.

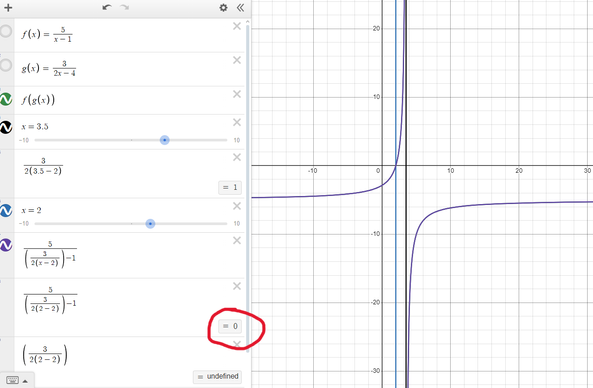
2. Desmos displays undefined, but internally it stores \(\infty\), as per the IEEE 754 standard. Then, \(\frac1\infty\) is considered to be \(0\), which is why that fraction is equal to \(0\). It doesn't store the value of \(\frac10\). Instead, it's stored as the Desmos-specific mathematical constant \(\infty\), roughly equal to \(10^{308}\). So, \(\frac{3}{2(2-2)}-1\) is about \(10^{308}\), and \(\frac{5}{10^{308}}\) is roughly \(0\), since all numbers in Desmos are rounded to \(15\) decimal points.

Here's an online calculator you can use to see how some values are represented in IEEE754 floating point!
https://www.h-schmidt.net/FloatConverter/IEEE754.html
#Desmos #IEEE754 #FloatingPoint #Error #FloatingPointError #FloatingPointNumber #Precision #Accuracy #Numbers #Maths #NumericalValues