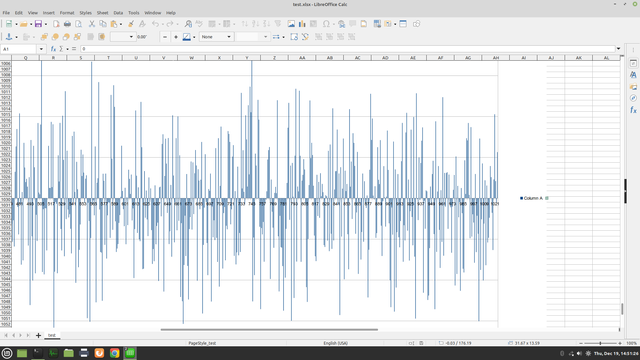
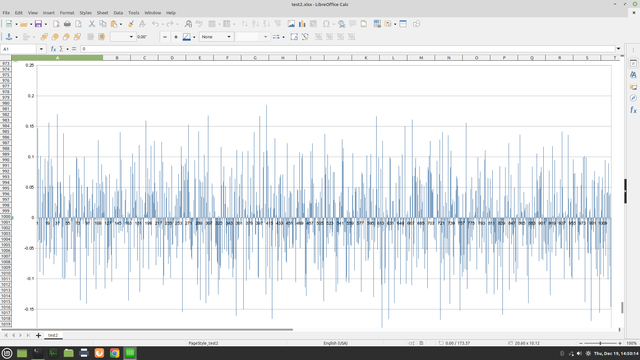
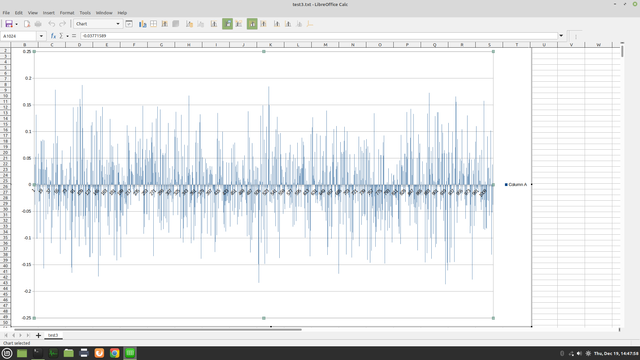
I have a measure of #irrationality, cranked my ratpak up to 1024 digits here are sqrt(2) sqrt(sqrt(2)) (sqrt(sqrt(sqrt(2))) note each nesting produces a less spiky #frequencyplot in other words sqrt(2) is closer to an undoing (^2) than the others, so yeah now I can search for constants we don't know how to write algebraically.
Client Info
Server: https://mastodon.social
Version: 2025.04
Repository: https://github.com/cyevgeniy/lmst