@rntz My point is that if you "solve" incremental maintenance of recursive definitions, you also solve GC. But we know GC is hard, so the generalized problem must be even harder. Also re "handles cycles but performs optimally if there are none", in GC land this would be something like "refcount, but with occasional GC", but this is predicated on the fact that you are allowed to overestimate the reachable set (and in general this may not be OK.)

@rntz Forgive me if this is obvious, but is this not the same as the refcounting / gc problem? (In which case, the true solution is to not play the game aka escape analysis)

The Aperiodic Monotile Earrings arrived! I made a Ko-fi Shop for them: https://ko-fi.com/s/5852007096

[Edit July 2: shipping to UK and Canada, can look into shipping elsewhere too!]

#aperiodic #monotile #mathstodon #mathart

This blog post on AI's effects on work skills by danah boyd is great.

I learned the concept of "moral crumple zones", introduced by Madeleine Elish. When an autonomous system, such as self-driving car, loses control, it assigns the control back to a human operator. It's too late for the human to do anything, but they will bear the moral and legal responsibility.

The human is the part of the self-driving car that is designated to absorb the moral impact on crash.

http://www.zephoria.org/thoughts/archives/2023/04/21/deskilling-on-the-job.html

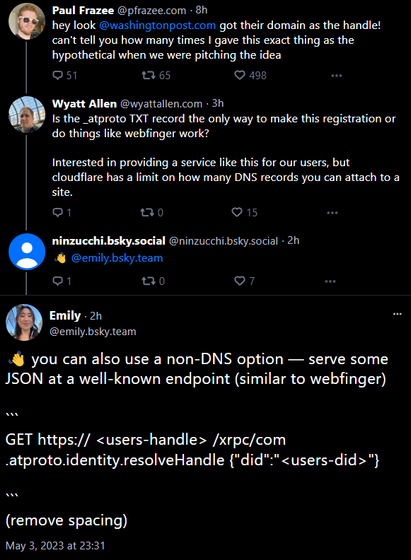
so on #Bluesky, rather than going with the well-documented and defined webfinger protocol, behind the .well-known directory, decided to make their own shit for verifying domains via HTTP (to change your handle to the website, proving your ownership of it)

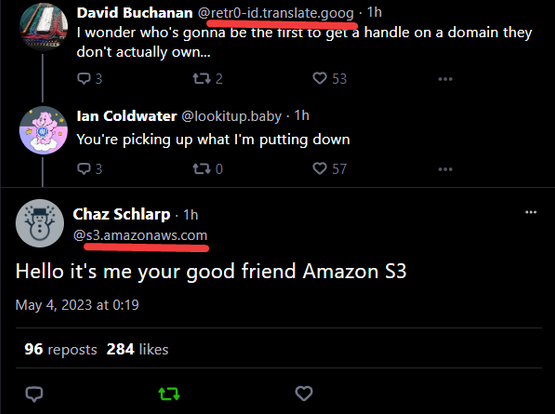
thus, somebody took the S3 bucket name "xrpc" and now is s3.amazonaws.com on the platform

going great

https://bsky.ipg.gay/profile/s3.amazonaws.com/post/3juud6zh5ur2n

oh neat, yoasobi did the op for oshinoko and i didn't even realize it when YouTube autoplay went on the MV until I was like "wait... I know these characters....."

Here's what you might get if you tell GPT3

"Prove or disprove: there exists a nowhere continuous function f whose absolute value is everywhere continuous."

It gave an answer in TeX, which someone typeset.

Because it looks like math, this answer is superficially persuasive. But it's complete bullshit. I soon found three fatal mistakes. For some reason I found the simplest one last.

First I became suspicious of the idea of finding infinitely many disjoint open intervals whose union is the real line. In fact this is impossible! Every open subset of ℝ is a disjoint union of countably many disjoint open intervals IN A UNIQUE WAY, and if that open subset is ℝ itself, that way uses just one open interval: (−∞, ∞).

That was an interesting mistake.

Then I noticed the claim that "|f| is bounded hence continuous everywhere", with no other justification. This is baloney.

Then I actually thought about the function f. Since f = |f|, there's no way |f| but not f can be continuous!

There are probably other mistakes but at that point I lost interest.

Is the moral that chatbots are hopeless at proving things?

No, GPT4 answered the same question quite well. It found the obvious example of a function that works: f(x) = 1 when x is rational and f(x) = -1 when x is irrational. It seems to have correctly proved that f is discontinuous everywhere. And it even acted like a typical mathematician, saying |f| is "obviously continuous everywhere, since it is constant".

Details:

https://nostalgebraist.tumblr.com/post/711802556830089216/update-tried-the-second-example-with-gpt-4-via

The optimal number of reverts is non-zero.

it's easy to see why people build unsound systems, it's so much easier than building sound systems

finished inputting all 32 of my IT-203-Fs into turbotax 😂

Branch cut the Monday after superbowl we are so good at this 🤓

As an OSS author, I secretly hope open source telemetry will actually become normalized, because I think it would be really useful, but I also doubt that it will ever actually happen

What kinds of performance problems in code would you expect NOT to be found by a profiler?

@rntz i gave up and retrained myself for per app

It’s very funny to me that the dominant Twentieth Century conception of AI was a slightly awkward nerd with an inhuman mastery of facts and logic, when what we actually got is smooth-talking bullshit artists who can’t do eighth-grade math.

@shapr sort of? My argument partner agreed that my interpretation of NY tax code looked right, but we also agreed that there was no way for NYS to actually tell if you'd done it correctly or not

gfd got nerd sniped into a taxes discussion AGAIN