Lmst

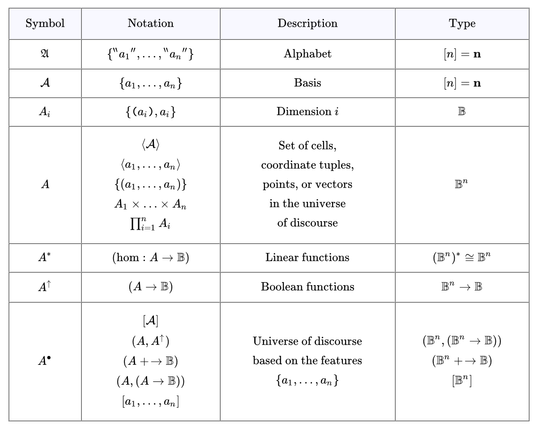
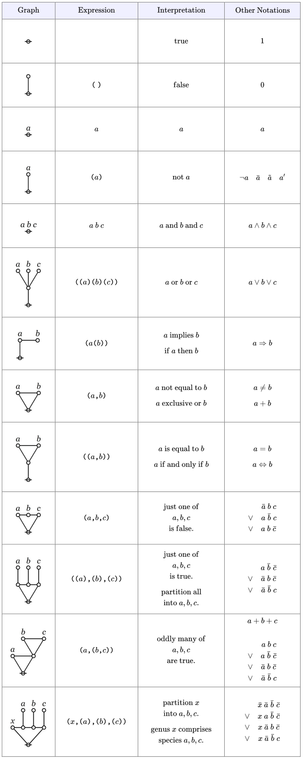
Differential Propositional Calculus • 10

Special Classes of Propositions (cont.)

Let’s pause at this point and get a better sense of how our special classes of propositions are structured and how they relate to propositions in general. We can do this by recruiting our visual imaginations and drawing up a sufficient budget of venn diagrams for each family of propositions. The case for 3 variables is exemplary enough for a start.

Linear Propositions

The linear propositions, may be written as sums:

One thing to keep in mind about these sums is that the values in are added “modulo 2”, that is, in such a way that

In a universe of discourse based on three boolean variables, the linear propositions take the shapes shown in Figure 8.

At the top is the venn diagram for the linear proposition of rank 3, which may be expressed by any one of the following three forms.

Next are the venn diagrams for the three linear propositions of rank 2, which may be expressed by the following three forms, respectively.

Next are the three linear propositions of rank 1, which are none other than the three basic propositions,

At the bottom is the linear proposition of rank 0, the everywhere false proposition or the constant function, which may be expressed by the form or by a simple

Resources

cc: Academia.edu • Cybernetics • Structural Modeling • Systems Science
cc: Conceptual Graphs • Laws of Form • Mathstodon • Research Gate

#Amphecks #Animata #BooleanAlgebra #BooleanFunctions #CSPeirce #CactusGraphs #CategoryTheory #Change #Cybernetics #DifferentialAnalyticTuringAutomata #DifferentialCalculus #DifferentialLogic #DiscreteDynamics #EquationalInference #FunctionalLogic #GraphTheory #Hologrammautomaton #IndicatorFunctions #InquiryDrivenSystems #Leibniz #Logic #LogicalGraphs #Mathematics #MinimalNegationOperators #PropositionalCalculus #Time #Topology #Visualization

Differential Propositional Calculus • 8
• https://inquiryintoinquiry.com/2024/12/07/differential-propositional-calculus-8-b/

Formal Development (cont.)

Before moving on, let's unpack some of the assumptions, conventions, and implications involved in the array of concepts and notations introduced above.

A universe of discourse A° = [a₁, …, aₙ] qualified by the logical features a₁, …, aₙ is a set A plus the set of all functions from the space A to the boolean domain B = {0, 1}. There are 2ⁿ elements in A, often pictured as the cells of a venn diagram or the nodes of a hypercube. There are 2^(2ⁿ) possible functions from A to B, accordingly pictured as all the ways of painting the cells of a venn diagram or the nodes of a hypercube with a palette of two colors.

A logical proposition about the elements of A is either true or false of each element in A, while a function f : A → B evaluates to 1 or 0 on each element of A. The analogy between logical propositions and boolean-valued functions is close enough to adopt the latter as models of the former and simply refer to the functions f : A → B as propositions about the elements of A.

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Differential Propositional Calculus • 7.2
• https://inquiryintoinquiry.com/2024/12/06/differential-propositional-calculus-7-b/

Formal Development (cont.)

Table 7 summarizes the basic notations needed to describe ordinary propositional calculi in a systematic fashion.

Table 7. Propositional Calculus • Basic Notation
• https://inquiryintoinquiry.files.wordpress.com/2020/02/propositional-calculus-basic-notation.png

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Differential Propositional Calculus • 6.2
• https://inquiryintoinquiry.com/2024/12/04/differential-propositional-calculus-6-b/

Cactus Calculus (cont.)

The briefest expression for logical truth is the empty word, denoted ε or λ in formal languages, where it forms the identity element for concatenation. It may be given visible expression in textual settings by means of the logically equivalent form (()), or, especially if operating in an algebraic context, by a simple 1. Also when working in an algebraic mode, the plus sign “+” may be used for exclusive disjunction. For example, we have the following paraphrases of algebraic expressions.

• x + y = (x, y)

• x + y + z = ((x, y), z) = (x, (y, z))

It is important to note the last expressions are not equivalent to the triple bracket (x, y, z).

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Differential Propositional Calculus • 6.1
• https://inquiryintoinquiry.com/2024/12/04/differential-propositional-calculus-6-b/

Cactus Calculus —

Table 6 outlines a syntax for propositional calculus based on two types of logical connectives, both of variable k‑ary scope.

• A bracketed sequence of propositional expressions (e₁, e₂, …, eₖ) is taken to mean exactly one of the propositions e₁, e₂, …, eₖ is false, in other words, their “minimal negation” is true.

• A concatenated sequence of propositional expressions e₁ e₂ … eₖ is taken to mean every one of the propositions e₁, e₂, …, eₖ is true, in other words, their “logical conjunction” is true.

Table 6. Syntax and Semantics of a Calculus for Propositional Logic
• https://inquiryintoinquiry.files.wordpress.com/2022/10/syntax-and-semantics-of-a-calculus-for-propositional-logic-4.0.png

All other propositional connectives may be obtained through combinations of the above two forms. As it happens, the concatenation form is dispensable in light of the bracket form but it is convenient to maintain it as an abbreviation for more complicated bracket expressions. While working with expressions solely in propositional calculus, it is easiest to use plain parentheses for bracket forms. In contexts where parentheses are needed for other purposes “teletype” parentheses (…) or barred parentheses (|…|) may be used for logical operators.

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Differential Propositional Calculus • 5
• https://inquiryintoinquiry.com/2024/12/03/differential-propositional-calculus-5-b/

Casual Introduction (concl.)

Table 5 exhibits the rules of inference responsible for giving the differential proposition dq its meaning in practice.

Table 5. Differential Inference Rules
• https://inquiryintoinquiry.files.wordpress.com/2020/02/differential-propositional-calculus-e280a2-differential-inference-rules.png

If the feature q is interpreted as applying to an object in the universe of discourse X then the differential feature dq may be taken as an attribute of the same object which tells it is changing “significantly” with respect to the property q — as if the object bore an “escape velocity” with respect to the condition q.

For example, relative to a frame of observation to be made more explicit later on, if q and dq are true at a given moment, it would be reasonable to assume ¬q will be true in the next moment of observation. Taken all together we have the fourfold scheme of inference shown above.

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Differential Inference Rules —

From ¬q and ¬dq infer ¬q next.
From ¬q and dq infer q next.
From q and ¬dq infer q next.
From q and dq infer ¬q next.

Differential Propositional Calculus • 4
• https://inquiryintoinquiry.com/2024/12/02/differential-propositional-calculus-4-b/

Casual Introduction (cont.)

In Figure 3 we saw how the basis of description for the universe of discourse X could be extended to a set of two qualities {q, dq} while the corresponding terms of description could be extended to an alphabet of two symbols {“q”, “dq”}.

Any propositional calculus over two basic propositions allows for the expression of 16 propositions all together. Salient among those propositions in the present setting are the four which single out the individual sample points at the initial moment of observation. Table 4 lists the initial state descriptions, using overlines to express logical negations.

Table 4. Initial State Descriptions
• https://inquiryintoinquiry.files.wordpress.com/2020/02/differential-propositional-calculus-e280a2-initial-state-descriptions.png

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Initial State Descriptions —

¬q and ¬dq describes a ;
¬q and dq describes d ;
q and ¬dq describes b ;
q and dq describes c .

Differential Propositional Calculus • 3.2
• https://inquiryintoinquiry.com/2024/12/01/differential-propositional-calculus-3-b/

Casual Introduction (cont.)

Figure 1 represents a universe of discourse X together with a basis of discussion {q} for expressing propositions about the contents of that universe. Once the quality q is given a name, say, the symbol “q”, we have the basis for a formal language specifically cut out for discussing X in terms of q. That language is more formally known as the “propositional calculus” with alphabet {“q”}.

In the context marked by X and {q} there are just four distinct pieces of information which can be expressed in the corresponding propositional calculus, namely, the constant proposition False, the negative proposition ¬q, the positive proposition q, and the constant proposition True.

For example, referring to the points in Figure 1, the constant proposition False holds of no points, the negative proposition ¬q holds of a and d, the positive proposition q holds of b and c, and the constant proposition True holds of all points in the sample.

Figure 3 preserves the same universe of discourse and extends the basis of discussion to a set of two qualities, {q, dq}. In corresponding fashion, the initial propositional calculus is extended by means of the enlarged alphabet, {“q”, “dq”}.

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Differential Propositional Calculus • 3.1
• https://inquiryintoinquiry.com/2024/12/01/differential-propositional-calculus-3-b/

Casual Introduction (cont.)

Figure 3 returns to the situation in Figure 1, but this time interpolates a new quality specifically tailored to account for the relation between Figure 1 and Figure 2.

Figure 3. Back, To The Future
• https://inquiryintoinquiry.files.wordpress.com/2023/11/differential-propositional-calculus-e280a2-figure-3.png

The new quality, dq, is marked as a “differential quality” on account of its absence or presence qualifying the absence or presence of change occurring in another quality. As with any quality, it is represented in the venn diagram by means of a “circle” distinguishing two halves of the universe of discourse, in this case, the portions of X outside and inside the region dQ.

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Differential Propositional Calculus • 2
• https://inquiryintoinquiry.com/2024/11/30/differential-propositional-calculus-2-b/

Casual Introduction (cont.)

Now consider the situation represented by the venn diagram in Figure 2.

Figure 2. Same Names, Different Habitations
• https://inquiryintoinquiry.files.wordpress.com/2023/11/differential-propositional-calculus-e280a2-figure-2.png

Figure 2 differs from Figure 1 solely in the circumstance that the object c is outside the region Q while the object d is inside the region Q.

Nothing says our encountering the Figures in the above order is other than purely accidental but if we interpret the sequence of frames as a “moving picture” representation of their natural order in a temporal process then it would be natural to suppose a and b have remained as they were with regard to the quality q while c and d have changed their standings in that respect. In particular, c has moved from the region where q is true to the region where q is false while d has moved from the region where q is false to the region where q is true.

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Differential Propositional Calculus • 1
• https://inquiryintoinquiry.com/2024/11/29/differential-propositional-calculus-1-b/

A “differential propositional calculus” is a propositional calculus extended by a set of terms for describing aspects of change and difference, for example, processes taking place in a universe of discourse or transformations mapping a source universe to a target universe.

Casual Introduction —

Consider the situation represented by the venn diagram in Figure 1.

Figure 1. Local Habitations, And Names
• https://inquiryintoinquiry.files.wordpress.com/2023/11/differential-propositional-calculus-e280a2-figure-1.png

The area of the rectangle represents the universe of discourse X. The universe under discussion may be a population of individuals having various additional properties or it may be a collection of locations occupied by various individuals. The area of the “circle” represents the individuals with the property q or the locations in the corresponding region Q. Four individuals, a, b, c, d, are singled out by name. As it happens, b and c currently reside in region Q while a and d do not.

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Differential Propositional Calculus • Overview 2
• https://inquiryintoinquiry.com/2024/11/27/differential-propositional-calculus-overview-b/

What follows is the outline of a sketch on differential propositional calculus intended as an intuitive introduction to the larger subject of differential logic, which amounts in turn to my best effort so far at dealing with the ancient and persistent problems of treating diversity and mutability in logical terms.

Note. I'll give just the links to the main topic heads below. Please follow the link at the top of the page for the full outline.

Part 1 —
• https://oeis.org/wiki/Differential_Propositional_Calculus_%E2%80%A2_Part_1

Casual Introduction
• https://oeis.org/wiki/Differential_Propositional_Calculus_%E2%80%A2_Part_1#Casual_Introduction

Cactus Calculus
• https://oeis.org/wiki/Differential_Propositional_Calculus_%E2%80%A2_Part_1#Cactus_Calculus

Part 2 —
• https://oeis.org/wiki/Differential_Propositional_Calculus_%E2%80%A2_Part_2

Formal_Development
• https://oeis.org/wiki/Differential_Propositional_Calculus_%E2%80%A2_Part_2#Formal_Development

Elementary Notions
• https://oeis.org/wiki/Differential_Propositional_Calculus_%E2%80%A2_Part_2#Elementary_Notions

Special Classes of Propositions
• https://oeis.org/wiki/Differential_Propositional_Calculus_%E2%80%A2_Part_2#Special_Classes_of_Propositions

Differential Extensions
• https://oeis.org/wiki/Differential_Propositional_Calculus_%E2%80%A2_Part_2#Differential_Extensions

Appendices —
• https://oeis.org/wiki/Differential_Propositional_Calculus_%E2%80%A2_Appendices

References —
• https://oeis.org/wiki/Differential_Propositional_Calculus_%E2%80%A2_References

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Differential Propositional Calculus • Overview 1
• https://inquiryintoinquiry.com/2024/11/27/differential-propositional-calculus-overview-b/

❝The most fundamental concept in cybernetics is that of “difference”, either that two things are recognisably different or that one thing has changed with time.❞

— W. Ross Ashby • An Introduction to Cybernetics

Differential logic is the component of logic whose object is the description of variation — the aspects of change, difference, distribution, and diversity — in universes of discourse subject to logical description. To the extent a logical inquiry makes use of a formal system, its differential component treats the use of a differential logical calculus — a formal system with the expressive capacity to describe change and diversity in logical universes of discourse.

In accord with the strategy of approaching logical systems in stages, first gaining a foothold in propositional logic and advancing on those grounds, we may set our first stepping stones toward differential logic in “differential propositional calculi” — propositional calculi extended by sets of terms for describing aspects of change and difference, for example, processes taking place in a universe of discourse or transformations mapping a source universe to a target universe.

#Peirce #Logic #LogicalGraphs #DifferentialLogic #DiscreteDynamicalSystems
#BooleanFunctions #BooleanDifferenceCalculus #CalculusOfLogicalDifferences
#PropositionalCalculus #DifferentialPropositionalCalculus #LogicalDynamics

Differential Logic • Overview 2
• https://inquiryintoinquiry.com/2024/11/25/differential-logic-overview-a/

Introduction
• https://oeis.org/wiki/Differential_Logic_%E2%80%A2_Part_1#Introduction

Cactus Language for Propositional Logic
• https://oeis.org/wiki/Differential_Logic_%E2%80%A2_Part_1#Cactus_Language_for_Propositional_Logic

Differential Expansions of Propositions
• https://oeis.org/wiki/Differential_Logic_%E2%80%A2_Part_1#Differential_Expansions_of_Propositions

Propositional Forms on Two Variables
• https://oeis.org/wiki/Differential_Logic_%E2%80%A2_Part_2#Propositional_Forms_on_Two_Variables

Transforms Expanded over Ordinary and Differential Variables
• https://oeis.org/wiki/Differential_Logic_%E2%80%A2_Part_2#Transforms_Expanded_over_Ordinary_and_Differential_Variables

Field Picture
• https://oeis.org/wiki/Differential_Logic_%E2%80%A2_Part_3#Field_Picture

Differential Fields
• https://oeis.org/wiki/Differential_Logic_%E2%80%A2_Part_3#Differential_Fields

Propositions and Tacit Extensions
• https://oeis.org/wiki/Differential_Logic_%E2%80%A2_Part_3#Propositions_and_Tacit_Extensions

Enlargement and Difference Maps
• https://oeis.org/wiki/Differential_Logic_%E2%80%A2_Part_3#Enlargement_and_Difference_Maps

Tangent and Remainder Maps
• https://oeis.org/wiki/Differential_Logic_%E2%80%A2_Part_3#Tangent_and_Remainder_Maps

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7/

#Peirce #Logic #Mathematics #LogicalGraphs #DifferentialLogic #DynamicSystems
#Inquiry #PropositionalCalculus #BooleanFunctions #BooleanDifferenceCalculus
#EquationalInference #MinimalNegationOperators #CalculusOfLogicalDifferences

Differential Logic • Overview 1
• https://inquiryintoinquiry.com/2024/11/25/differential-logic-overview-a/

A reader once told me “venn diagrams are obsolete” and of course we all know how unwieldy they become as our universes of discourse expand beyond four or five dimensions. Indeed, one of the first lessons I learned when I set about implementing Peirce's graphs and Spencer Brown's forms on the computer is that 2‑dimensional representations of logic quickly become death traps on numerous conceptual and computational counts.

Still, venn diagrams do us good service at the outset in visualizing the relationships among extensional, functional, and intensional aspects of logic. A facility with those connections is critical to the computational applications and statistical generalizations of propositional logic commonly used in mathematical and empirical practice. All things considered, then, it is useful to make as visible as possible the links between variant styles of imagery in logical representation — and that is what I hoped to do in the sketch of Differential Logic outlined below.

Note. I'll give just the links to the main topic heads in the next post. Please follow the link at the top of this post for the full outline.

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7/

#Peirce #Logic #Mathematics #LogicalGraphs #DifferentialLogic #DynamicSystems
#Inquiry #PropositionalCalculus #BooleanFunctions #BooleanDifferenceCalculus
#EquationalInference #MinimalNegationOperators #CalculusOfLogicalDifferences

Differential Logic • 1
• https://inquiryintoinquiry.com/2024/10/30/differential-logic-1-a/

Introduction —

Differential logic is the component of logic whose object is the description of variation — focusing on the aspects of change, difference, distribution, and diversity — in universes of discourse subject to logical description. A definition that broad naturally incorporates any study of variation by way of mathematical models, but differential logic is especially charged with the qualitative aspects of variation pervading or preceding quantitative models. To the extent a logical inquiry makes use of a formal system, its differential component governs the use of a “differential logical calculus”, that is, a formal system with the expressive capacity to describe change and diversity in logical universes of discourse.

Simple examples of differential logical calculi are furnished by “differential propositional calculi”. A differential propositional calculus is a propositional calculus extended by a set of terms for describing aspects of change and difference, for example, processes taking place in a universe of discourse or transformations mapping a source universe to a target universe. Such a calculus augments ordinary propositional calculus in the same way the differential calculus of Leibniz and Newton augments the analytic geometry of Descartes.

Resources —

Survey of Differential Logic
• https://inquiryintoinquiry.com/2024/02/25/survey-of-differential-logic-7/

cc: https://www.academia.edu/community/lJX2qa
cc: https://www.researchgate.net/post/Differential_Logic_The_Logic_of_Change_and_Difference

#Peirce #Logic #Mathematics #LogicalGraphs #DifferentialLogic #DynamicSystems
#Inquiry #PropositionalCalculus #BooleanFunctions #BooleanDifferenceCalculus
#EquationalInference #MinimalNegationOperators #CalculusOfLogicalDifferences

Logical Graphs • Formal Development 1
• https://inquiryintoinquiry.com/2024/09/12/logical-graphs-formal-development-1-a/

Recap —

A first approach to logical graphs was outlined in the article linked below.

Logical Graphs • First Impressions
• https://inquiryintoinquiry.com/2024/08/26/logical-graphs-first-impressions-a/

That introduced the initial elements of logical graphs and hopefully supplied the reader with an intuitive sense of their motivation and rationale.

Formal Development —

Logical graphs are next presented as a formal system by going back to the initial elements and developing their consequences in a systematic manner.

The next order of business is to give the precise axioms used to develop the formal system of logical graphs. The axioms derive from C.S. Peirce's various systems of graphical syntax via the “calculus of indications” described in Spencer Brown's “Laws of Form”. The formal proofs to follow will use a variation of Spencer Brown's annotation scheme to mark each step of the proof according to which axiom is called to license the corresponding step of syntactic transformation, whether it applies to graphs or to strings.

Resources —

Survey of Animated Logical Graphs
• https://inquiryintoinquiry.com/2024/03/18/survey-of-animated-logical-graphs-7/

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus

Logical Graphs • First Impressions 1
• https://inquiryintoinquiry.com/2024/08/30/logical-graphs-first-impressions-1/

Moving Pictures of Thought —

A logical graph is a graph‑theoretic structure in one of the systems of graphical syntax Charles S. Peirce developed for logic.

Introduction —

In numerous papers on qualitative logic, entitative graphs, and existential graphs, C.S. Peirce developed several versions of a graphical formalism, or a graph‑theoretic formal language, designed to be interpreted for logic.

In the century since Peirce initiated their line of development, a variety of formal systems have branched out from what is abstractly the same formal base of graph‑theoretic structures. The posts to follow explore the common basis of those formal systems from a bird's eye view, focusing on the aspects of form shared by the entire family of algebras, calculi, or languages, however they happen to be viewed in a given application.

Resources —

Logical Graphs
• https://oeis.org/wiki/Logical_Graphs

Futures Of Logical Graphs
• https://oeis.org/wiki/Futures_Of_Logical_Graphs

Propositional Equation Reasoning Systems
• https://oeis.org/wiki/Propositional_Equation_Reasoning_Systems

Charles Sanders Peirce • Bibliography
• https://mywikibiz.com/Charles_Sanders_Peirce
• https://mywikibiz.com/Charles_Sanders_Peirce_%28Bibliography%29

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus

Transformations of Logical Graphs • Discussion 1
• https://inquiryintoinquiry.com/2024/05/22/transformations-of-logical-graphs-discussion-1/

Re: Laws of Form
• https://groups.io/g/lawsofform/topic/transformations_of_logical/105927945

Mauro Bertani
• https://groups.io/g/lawsofform/message/3204

Dear Mauro,

The couple of pages linked below give the clearest and quickest introduction I've been able to manage so far when it comes to the elements of logical graphs, at least, in the way I've come to understand them. The first page gives a lot of detail by way of motivation and computational implementation, so you could easily put that off till you feel a need for it. The second page lays out the precise axioms or initials I use — the first algebraic axiom varies a bit from Spencer Brown for a better fit with C.S. Peirce — and also shows the parallels between the dual interpretations.

Logical Graphs • First Impressions
• https://inquiryintoinquiry.com/2023/08/24/logical-graphs-first-impressions/

Logical Graphs • Formal Development
• https://inquiryintoinquiry.com/2023/09/01/logical-graphs-formal-development-a/

Additional Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Animated Logical Graphs
• https://inquiryintoinquiry.com/2024/03/18/survey-of-animated-logical-graphs-7/

Survey of Semiotics, Semiosis, Sign Relations
• https://inquiryintoinquiry.com/2024/01/26/survey-of-semiotics-semiosis-sign-relations-5/

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus
#CactusSyntax #MinimalNegationOperators #MathematicalDuality #Form

Mathematical Duality in Logical Graphs • Discussion 2.2
• https://inquiryintoinquiry.com/2024/05/04/mathematical-duality-in-logical-graphs-discussion-2/

What you say about deriving arithmetic, algebra, group theory, and all the rest from the calculus of indications may well be true, but it remains to be shown if so, and that's aways down the road from here.

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Logical Graphs • First Impressions
• https://inquiryintoinquiry.com/2023/08/24/logical-graphs-first-impressions/

Logical Graphs • Formal Development
• https://inquiryintoinquiry.com/2023/09/01/logical-graphs-formal-development-a/

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus
#CactusSyntax #MinimalNegationOperators #MathematicalDuality #Form

#BooleanFunctions

Client Info