@MathOutLoud

if exactly one of A, B is true then C is true.

In #CactusSyntax —

((A),(B)) = exactly one of A, B is true

= (A, B) = exactly one of A, B is false.

(P (Q)) = if P then Q.

((A, B)(C)) = proposition in question.

suppose C = false = ().

then the propostion in question = ((A, B)).

i.e. A = B.

Transformations of Logical Graphs • Discussion 1
• https://inquiryintoinquiry.com/2024/05/22/transformations-of-logical-graphs-discussion-1/

Re: Laws of Form
• https://groups.io/g/lawsofform/topic/transformations_of_logical/105927945

Mauro Bertani
• https://groups.io/g/lawsofform/message/3204

Dear Mauro,

The couple of pages linked below give the clearest and quickest introduction I've been able to manage so far when it comes to the elements of logical graphs, at least, in the way I've come to understand them. The first page gives a lot of detail by way of motivation and computational implementation, so you could easily put that off till you feel a need for it. The second page lays out the precise axioms or initials I use — the first algebraic axiom varies a bit from Spencer Brown for a better fit with C.S. Peirce — and also shows the parallels between the dual interpretations.

Logical Graphs • First Impressions
• https://inquiryintoinquiry.com/2023/08/24/logical-graphs-first-impressions/

Logical Graphs • Formal Development
• https://inquiryintoinquiry.com/2023/09/01/logical-graphs-formal-development-a/

Additional Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Survey of Animated Logical Graphs
• https://inquiryintoinquiry.com/2024/03/18/survey-of-animated-logical-graphs-7/

Survey of Semiotics, Semiosis, Sign Relations
• https://inquiryintoinquiry.com/2024/01/26/survey-of-semiotics-semiosis-sign-relations-5/

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus
#CactusSyntax #MinimalNegationOperators #MathematicalDuality #Form

Mathematical Duality in Logical Graphs • Discussion 2.2
• https://inquiryintoinquiry.com/2024/05/04/mathematical-duality-in-logical-graphs-discussion-2/

What you say about deriving arithmetic, algebra, group theory, and all the rest from the calculus of indications may well be true, but it remains to be shown if so, and that's aways down the road from here.

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Logical Graphs • First Impressions
• https://inquiryintoinquiry.com/2023/08/24/logical-graphs-first-impressions/

Logical Graphs • Formal Development
• https://inquiryintoinquiry.com/2023/09/01/logical-graphs-formal-development-a/

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus
#CactusSyntax #MinimalNegationOperators #MathematicalDuality #Form

Mathematical Duality in Logical Graphs • 1.2
• https://inquiryintoinquiry.com/2024/05/03/mathematical-duality-in-logical-graphs-1/

It was in this context that Peirce's systems of logical graphs developed, issuing in dual interpretations of the same formal axioms which Peirce referred to as “entitative graphs” and “existential graphs”, respectively. He developed only the existential interpretation to any great extent, since the extension from propositional to relational calculus appeared more natural in that case, but whether there is any logical or mathematical reason for the symmetry to break at that point is a good question for further research.

Resources —

Duality Indicating Unity
• https://inquiryintoinquiry.com/2013/01/31/duality-indicating-unity-1/

C.S. Peirce • Logic of Number
• https://inquiryintoinquiry.com/2012/09/01/c-s-peirce-logic-of-number-ms-229/

C.S. Peirce • Syllabus • Selection 1
• https://inquiryintoinquiry.com/2014/08/24/c-s-peirce-syllabus-selection-1/

References —

• Peirce, C.S., [Logic of Number — Le Fevre] (MS 229), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 2, 592–595.

• Spencer Brown, G. (1969), Laws of Form, George Allen and Unwin, London, UK.

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus
#CactusSyntax #MinimalNegationOperators #MathematicalDuality #Form

Mathematical Duality in Logical Graphs • 1.1
• https://inquiryintoinquiry.com/2024/05/03/mathematical-duality-in-logical-graphs-1/

“All other sciences without exception depend upon the principles of mathematics; and mathematics borrows nothing from them but hints.”

— C.S. Peirce • “Logic of Number”

“A principal intention of this essay is to separate what are known as algebras of logic from the subject of logic, and to re‑align them with mathematics.”

— G. Spencer Brown • “Laws of Form”

The duality between entitative and existential interpretations of logical graphs tells us something important about the relation between logic and mathematics. It tells us the mathematical forms giving structure to reasoning are deeper and more abstract at once than their logical interpretations.

A formal duality points to a more encompassing unity, founding a calculus of forms whose expressions can be read in alternate ways by switching the meanings assigned to a pair of primitive terms. Spencer Brown's mathematical approach to “Laws of Form” and the whole of Peirce's work on the mathematics of logic shows both thinkers were deeply aware of this principle.

Peirce explored a variety of dualities in logic which he treated on analogy with the dualities in projective geometry. This gave rise to formal systems where the initial constants, and thus their geometric and graph‑theoretic representations, had no uniquely fixed meanings but could be given dual interpretations in logic.

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus
#CactusSyntax #MinimalNegationOperators #MathematicalDuality #Form

Operator Variables in Logical Graphs • Discussion 1
• https://inquiryintoinquiry.com/2024/04/08/operator-variables-in-logical-graphs-discussion-1/

Re: Operator Variables in Logical Graphs • 1
• https://inquiryintoinquiry.com/2024/04/06/operator-variables-in-logical-graphs-1/

Re: Academia.edu • Stephen Duplantier
• https://www.academia.edu/community/Lxn1Ww?c=yq1Rxy

SD:
❝The best way for me to read Peirce is as if he was writing poetry. So if his algebra is poetry — I imagine him approving of the approach since he taught me abduction in the first place — there is room to wander. With this, I venture the idea that his “wide field” is a local algebraic geography far from the tended garden. There, where weeds and wild things grow and hybridize are the non‑dichotomic mathematics.❞

Stephen,

“Abdeuces Are Wild”, as they say, maybe not today, maybe not tomorrow, but soon …

As far as my own guess, and a lot of my wandering in pursuit of it goes, I'd venture Peirce's field of vision opens up not so much from dichotomic to trichotomic domains of value as from dyadic to triadic relations, and all that with particular significance into the medium of reflection afforded by triadic sign relations.

Resources —

Logic Syllabus
• https://inquiryintoinquiry.com/logic-syllabus/

Semeiotic
• https://oeis.org/wiki/Semeiotic

Sign Relations
• https://oeis.org/wiki/Sign_relation

Triadic Relations
• https://oeis.org/wiki/Triadic_relation

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus
#CactusSyntax #MinimalNegationOperators #LogicalOperatorVariables

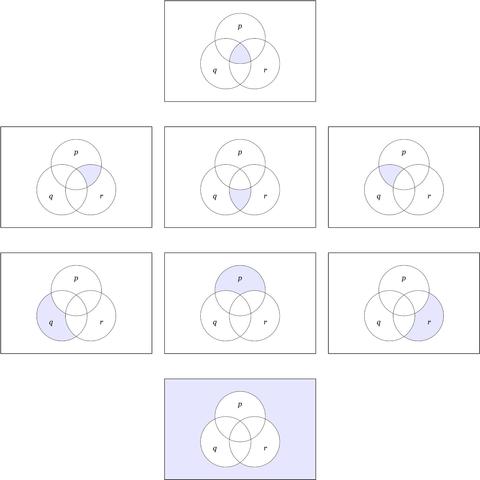
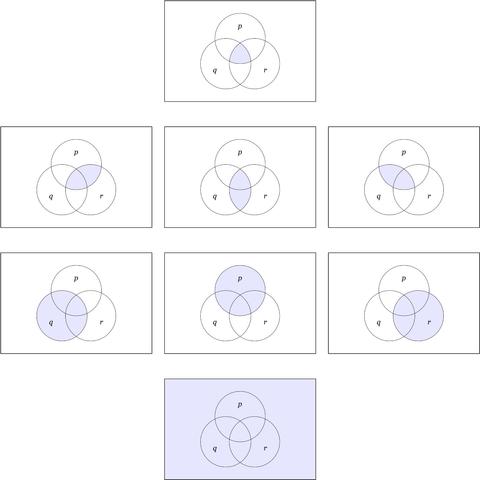
Operator Variables in Logical Graphs • 1.2
• https://inquiryintoinquiry.com/2024/04/06/operator-variables-in-logical-graphs-1/

Consider De Morgan's rules:

• ¬(A ∧ B) = ¬A ∨ ¬B

• ¬(A ∨ B) = ¬A ∧ ¬B

The common form exhibited by the two rules could be captured in a single formula by taking “o₁” and “o₂” as variable names ranging over a family of logical operators, then asking what substitutions for o₁ and o₂ would satisfy the following equation.

• ¬(A o₁ B) = ¬A o₂ ¬B

We already know two solutions to this “operator equation”, namely, (o₁, o₂) = (∧, ∨) and (o₁, o₂) = (∨, ∧). Wouldn't it be just like Peirce to ask if there are others?

Having broached the subject of “logical operator variables”, I will leave it for now in the same way Peirce himself did:

❝I shall not further enlarge upon this matter at this point, although the conception mentioned opens a wide field; because it cannot be set in its proper light without overstepping the limits of dichotomic mathematics.❞ (Peirce, CP 4.306).

Further exploration of operator variables and operator invariants treads on grounds traditionally known as second intentional logic and “opens a wide field”, as Peirce says. For now, however, I will tend to that corner of the field where our garden variety logical graphs grow, observing the ways in which operative variations and operative themes naturally develop on those grounds.

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus
#CactusSyntax #MinimalNegationOperators #LogicalOperatorVariables

Operator Variables in Logical Graphs • 1.1
• https://inquiryintoinquiry.com/2024/04/06/operator-variables-in-logical-graphs-1/

In lieu of a field study requirement for my bachelor's degree I spent two years in various state and university libraries reading everything I could find by and about Peirce, poring most memorably through reels of microfilmed Peirce manuscripts Michigan State had at the time, all in trying to track down some hint of a clue to a puzzling passage in Peirce's “Simplest Mathematics”, most acutely coming to a head with that bizarre line of type at CP 4.306, which the editors of Peirce's “Collected Papers”, no doubt compromised by the typographer's reluctance to cut new symbols, transmogrified into a script more cryptic than even the manuscript's original hieroglyphic.

I found one key to the mystery in Peirce's use of “operator variables”, which he and his students Christine Ladd‑Franklin and O.H. Mitchell explored in depth. I will shortly discuss that theme as it affects logical graphs but it may be useful to give a shorter and sweeter explanation of how the basic idea typically arises in common logical practice.

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus
#CactusSyntax #MinimalNegationOperators #LogicalOperatorVariables

Survey of Animated Logical Graphs • 7
• https://inquiryintoinquiry.com/2024/03/18/survey-of-animated-logical-graphs-7/

This is a Survey of blog and wiki posts on Logical Graphs, encompassing several families of graph‑theoretic structures originally developed by Charles S. Peirce as graphical formal languages or visual styles of syntax amenable to interpretation for logical applications.

Please follow the above link for the full set of resources.
Articles and blog series on the core ideas are linked below.

Beginnings —

Logical Graphs • First Impressions
• https://inquiryintoinquiry.com/2023/08/24/logical-graphs-first-impressions/

Logical Graphs • Formal Development
• https://inquiryintoinquiry.com/2023/09/01/logical-graphs-formal-development-a/

Elements —

Logic Syllabus
• https://oeis.org/wiki/Logic_Syllabus

Logical Graphs
• https://oeis.org/wiki/Logical_Graphs

Minimal Negation Operators
• https://oeis.org/wiki/Minimal_negation_operator

Propositional Equation Reasoning Systems
• https://oeis.org/wiki/Propositional_Equation_Reasoning_Systems

Examples —

Peirce's Law
• https://inquiryintoinquiry.com/2023/10/18/peirces-law-a/
• https://oeis.org/wiki/Peirce%27s_law

Praeclarum Theorema
• https://inquiryintoinquiry.com/2023/10/05/praeclarum-theorema-a/
• https://oeis.org/wiki/Logical_Graphs#Praeclarum_theorema

Proof Animations
• https://oeis.org/wiki/User:Jon_Awbrey/ANIMATION#Proof_Animations

Excursions —

Cactus Language
• https://oeis.org/wiki/Cactus_Language_%E2%80%A2_Overview

Futures Of Logical Graphs
• https://oeis.org/wiki/Futures_Of_Logical_Graphs

Applications —

Applications of a Propositional Calculator • Constraint Satisfaction Problems
• https://www.academia.edu/4727842/Applications_of_a_Propositional_Calculator_Constraint_Satisfaction_Problems

Exploratory Qualitative Analysis of Sequential Observation Data
• https://oeis.org/wiki/User:Jon_Awbrey/Exploratory_Qualitative_Analysis_of_Sequential_Observation_Data

Differential Analytic Turing Automata
• https://oeis.org/wiki/Differential_Analytic_Turing_Automata_%E2%80%A2_Overview

Survey of Theme One Program
• https://inquiryintoinquiry.com/2024/02/26/survey-of-theme-one-program-6/

#Peirce #Logic #LogicalGraphs #EntitativeGraphs #ExistentialGraphs
#SpencerBrown #LawsOfForm #BooleanFunctions #PropositionalCalculus
#CactusSyntax #MinimalNegationOperator #PeircesLaw #TuringAutomata

Cactus Rules
• https://oeis.org/wiki/User:Jon_Awbrey/Cactus_Rules

With an eye toward the aims of the NKS Forum I've begun to work out a translation of the “elementary cellular automaton rules” (ECARs), in effect, just the boolean functions of abstract type \(f : \mathbb{B}^3 \to \mathbb{B},\) into cactus language, and I'll post a selection of my working notes here.

#Logic #LogicalGraphs #BooleanFunctions #PropositionalCalculus
#CactusCalculus #CactusLanguage #CactusSyntax #CellularAutomata

#MinimalNegationOperators
• https://oeis.org/wiki/Minimal_negation_operator

#Peirce #LogicalGraphs #MinimalNegations
#BooleanFunctions #PropositionalCalculus
#CactusGraphs #CactusLanguage #CactusSyntax

@somedonkey @NicoleCRust

#CactusLanguage #CactusSyntax
• https://oeis.org/wiki/Cactus_Language_%E2%80%A2_Overview

@charlient

Try Cacti —

#CactusLanguage
• https://oeis.org/wiki/Cactus_Language_•_Overview

#CactusGraphs #CactusSyntax

#ThemeOneProgram • #JetsAndSharks 2
• https://inquiryintoinquiry.com/2022/08/30/theme-one-program-jets-and-sharks-2/

As we saw last time, Theme One reads the text file shown below and constructs a #CactusGraph #DataStructure in computer memory. The cactus graph represents a single #LogicalFormula in #PropositionalCalculus which embodies all the #LogicalConstraints defining the Jets and Sharks #DataBase.

Jets and Sharks • Log File
• https://inquiryintoinquiry.files.wordpress.com/2022/08/theme-one-guide-e280a2-jets-and-sharks-e280a2-log-file.png

#Logic #LogicalGraphs #Peirce
#CactusSyntax #LogicalCacti
#MinimalNegationOperators

#ThemeOneProgram • #JetsAndSharks 1.5
• https://inquiryintoinquiry.com/2022/08/25/theme-one-program-jets-and-sharks-1/

Reference —

#McClelland, J.L. (2015),
Explorations in #ParallelDistributedProcessing :
A Handbook of Models, Programs, and Exercises, 2nd ed. (draft),
#StanfordParallelDistributedProcessingLab.
• https://web.stanford.edu/group/pdplab/
#PDPHandbook Online —
• https://web.stanford.edu/group/pdplab/pdphandbook/
Section 2.3 —
• https://web.stanford.edu/group/pdplab/pdphandbook/handbookch3#x7-320002.3
Figure 2.1 —
• https://web.stanford.edu/group/pdplab/pdphandbook/jetsandsharkstable.png

#Logic #LogicalGraphs #Peirce
#CactusSyntax #LogicalCacti
#MinimalNegationOperators

#ThemeOneProgram • #JetsAndSharks 1.4
• https://inquiryintoinquiry.com/2022/08/25/theme-one-program-jets-and-sharks-1/

Displayed below is the text expression of a #TraversalString which Theme One parses into a #CactusGraph #DataStructure in computer memory. The cactus graph represents a single #LogicalFormula in #PropositionalCalculus which embodies all the #LogicalConstraints defining the Jets & Sharks #DataBase.

Log File
• https://inquiryintoinquiry.files.wordpress.com/2022/08/theme-one-guide-e280a2-jets-and-sharks-e280a2-log-file.png

#Logic #LogicalGraphs #Peirce
#CactusSyntax #LogicalCacti
#MinimalNegationOperators

#DifferentialPropositionalCalculus • 7.2
• https://inquiryintoinquiry.com/2020/03/05/differential-propositional-calculus-7/

In a #UniverseOfDiscourse based on 3 #BooleanVariables \(p,q,r\) there are \(2^3=8\) #SingularPropositions. Their #VennDiagrams are shown in Figure 10.

\(\text{Figure 10. Singular Propositions} : \mathbb{B}^3 \to\mathbb{B}\)
• https://inquiryintoinquiry.files.wordpress.com/2020/03/venn-diagrams-e280a2-p-q-r-e280a2-singular-propositions.jpg

Related Subjects —
#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions
#CactusSyntax #MinimalNegationOperators
#DiscreteDynamics #QualitativeDynamics

#DifferentialPropositionalCalculus • 6.2
• https://inquiryintoinquiry.com/2020/03/02/differential-propositional-calculus-6/

Figure 9. #VennDiagrams for #PositivePropositions on 3 Variables
• https://inquiryintoinquiry.files.wordpress.com/2020/03/venn-diagrams-e280a2-p-q-r-e280a2-positive-propositions.jpg

Rank 3 (Top). The #BooleanProduct or #LogicalConjunction \(pqr.\)

Rank 2. The 3 #BooleanProducts \(pr, qr, pq.\)

Rank 1. The 3 #BasicPropositions \(q, p, r.\)

Rank 0 (Bottom). The #ConstantFunction \(1 : \mathbb{B}^3 \to \mathbb{B}\) or the #ConstantProposition expressed in #CactusSyntax by the form \(\texttt{((}~\texttt{))}.\)

#Logic

#DifferentialPropositionalCalculus • 6.1
• https://inquiryintoinquiry.com/2020/03/02/differential-propositional-calculus-6/

In a #UniverseOfDiscourse based on 3 #BooleanVariables \(p, q, r\) there are \(2^3 = 8\) #PositivePropositions. Their #VennDiagrams are shown in Figure 9.

\(\text{Figure 9. Positive Propositions} : \mathbb{B}^3 \to \mathbb{B}\)
• https://inquiryintoinquiry.files.wordpress.com/2020/03/venn-diagrams-e280a2-p-q-r-e280a2-positive-propositions.jpg

#Logic #LogicalGraphs #DifferentialLogic
#PropositionalCalculus #BooleanFunctions
#CactusSyntax #MinimalNegationOperators
#DiscreteDynamics #QualitativeDynamics

#DifferentialPropositionalCalculus • 5.6
• https://inquiryintoinquiry.com/2020/02/29/differential-propositional-calculus-5/

\(\text{Figure 8. Linear Propositions} : \mathbb{B}^3 \to \mathbb{B}\)
• https://inquiryintoinquiry.files.wordpress.com/2020/02/venn-diagrams-e280a2-p-q-r-e280a2-linear-propositions.jpg

At the bottom of Figure 8 is #VennDiagram for the #LinearProposition of rank 0, the constant \(0\) function or the everywhere false proposition, expressed in #CactusSyntax by the form \(\texttt{(}~\texttt{)}\) or in algebraic form by a simple \(0.\)

\(\text{Figure 8.4 Venn Diagram for}~\texttt{(}~\texttt{)}\)