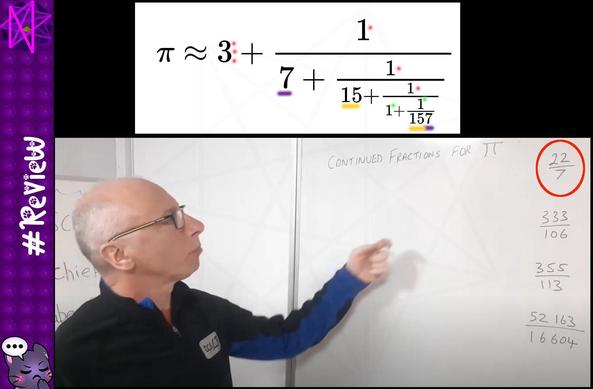
Today, while I waited for my appointment, I found this vid about continued fractions << https://www.youtube.com/watch?v=h-oETs62tWU >>. The author discusses several approximations for pi, but the best one isn't visually appealing. 1/2 #pi #continuedfractions #nomxd #Review🐾

In (canonical, simple) Continued Fraction (CFs) representation, every real number is a list starting with an integer 𝑎₀ and followed by some number (possibly none) of positive integers [𝑎₁, 𝑎₂, ...]. In strictly typed programming languages, this is essentially a non-empty list; for example, in Haskell, one can use Data.List.NonEmpty and the CF becomes (𝑎₀ :| [𝑎₁, 𝑎₂, ...]) = (𝑎₀ :| tail).

Haskell's strict typing enforces the non-empty aspect of CFs. The CF list must be non-empty, so we can think of it as a head (the 𝑎₀ term) and a (possibly empty) tail (the [𝑎₁, 𝑎₂, ...] terms). If the tail is empty, then the number is an integer. So the natural numbers 0, 1, 2, ... become (0 :| []), (1 :| []), (2 :| []) and so on in CF representation.

Now, taking reciprocal in CF representation involves either removing 𝑎₀ if it is 0, or prepending 0 to the whole list. Focusing on the first case, if 𝑎₀ is 0, then we remove that from the list and keep only the tail terms. This step combined with strict typing shows why there is no reciprocal of 0.

If we start with (0 :| []), remove 0 and only keep the tail then we are left with just the empty list []. However, every real number corresponds to a non-empty list and CFs don't allow empty lists.

Therefore the reciprocal of 0 is not a real number.

#math #ContinuedFractions #type #theory #haskell #FunctionalPrograming

@jamestanton@twitter.com (https://gdaymath.com/) writes (https://twitter.com/jamestanton/status/1613485564006637568):
“It is impossible to draw an equilateral triangle on a square lattice of dots with each vertex on a dot. (Why?) But can we get close?

Is it possible to have two vertices on a dot and the third within 0.00000001 units from a dot?

(The picture is not equilateral.)”

#geometry #math #ContinuedFractions #ApproximateInteger #PicksTheorem

I love the hidden patterns revealed in #ContinuedFractions Here is Euler's number e which is in fact transcendental, whose decimal expansion seems random, but look at the beautiful pattern in the coefficients. From an #Android app I made for myself. #math #numbertheory

Mathematically, I'm most interested in #NumberTheory (years ago did some research related to #ContinuedFractions). I love the numbers #phi, #pi, and #e, and the various days celebrating them! I enjoy #geometry and #discretemath recreationally too. CS/engineering-wise, I'm most interested in #ai #artificialintelligence and #MachineLearning, #robotics and #automation, #Android #appdev, #cybersecurity, #softwaredevelopment, and more!

https://boffosocko.com/2022/09/28/theory-and-applications-of-continued-fractions-math-x-451-50-fall-2022/

Last few nights I've been working on another mental calculation. In this episode of #CountingSheep, I bring you #PellsEquation and #ContinuedFractions.