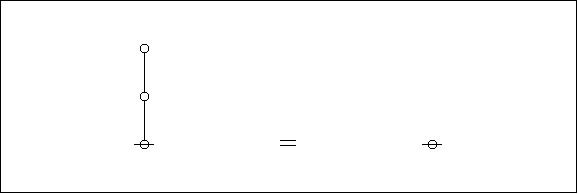#LogicalGraphs • 17
• https://oeis.org/w/index.php?title=Logical_Graphs&stable=0&redirect=no#Duality
#Duality • Logical and Topological
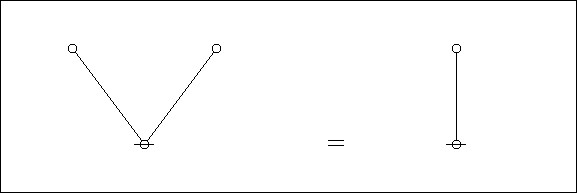
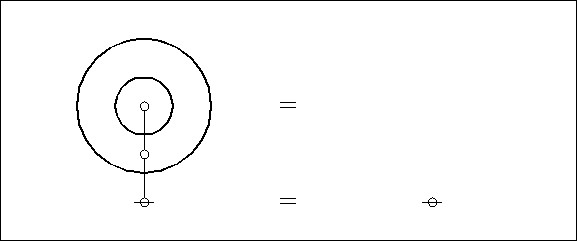
Editing the composite picture of #AlphaGraphs and #DualGraphs in Figure 8 to bring out the dual graphs by themselves affords a view of the first #InitialEquation shown in Figure 9.
Figure 9
• https://oeis.org/w/images/8/85/Logical_Graph_Figure_9_Visible_Frame.jpg
#Logic #Peirce #SpencerBrown #LawsOfForm
#PropositionalCalculus #BooleanFunctions
#GraphTheory #ModelTheory #ProofTheory