Lmst

Introduction

Measures of central tendency like mean, median and mode might not give you the complete picture of the data. They do not give you the info about variability and dispersion of the data. Understanding data distribution is a crucial aspect of statistics, especially in medical research, where making sense of data is often the key to discovering new insights. One of the most informative and robust measures of dispersion is the Interquartile Range (IQR).

In this post, we’ll dive deep into what the IQR is, why it’s important, and how to calculate it using various tools like Google Sheets, Excel, and even manually. Whether you’re just starting out or brushing up on your statistical knowledge, this guide will help you master the IQR.

What is the Interquartile Range?

The Interquartile Range (IQR) is a measure of dispersion or variability that describes the range within which the middle 50% of your data lies.

Unlike the range, which considers all data points, the IQR focuses on the central portion, making it less sensitive to outliers and more reflective of the data’s overall spread.
Just like median is a robust measure of central tendency which is often used in skewed data, interquartile range is especially useful in skewed data to measure dispersion or variability of the data.
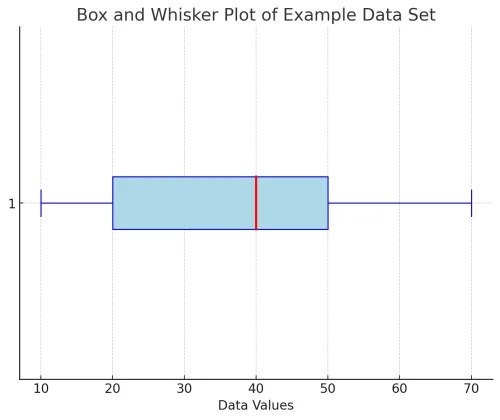
Example of a graphical representation of the data set: 10, 15, 20, 35, 40, 50, 55, 70.

Understanding Quartiles

To grasp the IQR, you need to understand quartiles. Arrange the values in your dataset in ascending order and imagine dividing the entire data set into four equal parts. The first quartile or Q1

Q1 (First Quartile): This is the median of the lower half of the data set. This lowest quartile or Q1 represents the 25th percentile of the dataset.
Q2 (Second Quartile): This is simply the median of the data set, marking the 50th percentile.
Q3 (Third Quartile): This is the median of the upper half of the data set, marking the 75th percentile.

The IQR is calculated as:

This formula subtracts the first quartile from the third quartile, giving you the range of the middle 50% of your data.

Why is the Interquartile Range Important?

The IQR is a robust measure of variability and is particularly useful when dealing with skewed distributions or data with outliers.
Since it focuses on the central portion of the data, it provides a better sense of the typical spread than the full range, which might be distorted by extreme values.
Example: Imagine you’re analyzing the blood pressure readings of a group of patients. If a few patients have abnormally high or low blood pressure, the IQR will give you a better understanding of the “normal” range for most patients, rather than being skewed by the extremes.

Note Before you learn Calculating the Interquartile Range

The smallest value that is greater than k percent of the values.
The smallest value that is greater than or equal to k percent of values.
An interpolated value between the two closest ranks

As you have learnt by now, the Interquartile range depends on the quartiles – Q1, Q2, Q3. These quartiles are nothing but percentiles in the dataset. However there is no consensus among statisticians about the exact formula or definition to calculate percentiles. The three calculation methods define the kth percentile in the following slightly different ways:

By using these methods, one can get slightly different values for the same percentile. So different methods and statistical software programs will find slightly different Q1 and Q3 values, which affects the interquartile range. These variations stem from alternate ways of finding percentiles.

How do we calculate the percentiles?

When you calculate quartiles using excel or google sheets or just any statistical software, you will come across terms like quartile inclusive and quartile exclusive Let me try to make this stuff simpler.

Consider the following dataset: 10, 15, 20, 35, 40, 50, 55, 70.

In the above dataset, by following the definition of median, 40 is determined as median.
In the exclusive method, the median is excluded from the calculation of Q1 and Q3. This method divides the data set into two halves, excluding the median (40 in the above example) and then calculates the quartiles from these halves.
Q1 (25th percentile): The median of the lower half, excluding the median of the entire data set is 17.5
Q3 (75th percentile): The median of the upper half, excluding the median of the entire data set is 52.5
The excel or google sheets formula for exclusive quartiles is = QUARTILE.EXC (data range, quart).
- Eg, = QUARTILE.EXC (A1:A9, 1)
The exclusive method also doesn’t consider the extreme value of each half. So by using this formula you simple cannot calculate Q0 or Q4. Both of them will result in an error.

The exclusive method is more common in inferential statistics and is preferred when working with larger data sets. It provides a more focused view of the data’s distribution by excluding the central value and emphasizing the spread of the data.

In the inclusive method, the quartiles are calculated by including the median in the calculation of both the lower and upper quartiles. This method treats the data set as a whole and ensures that all values, including the median, contribute to the calculation of Q1 (first quartile) and Q3 (third quartile).

Q1 (25th percentile): Using the inclusive method, Q1 is the median of the lower half of the data set, including the median of the entire data set. 20 is the Q1 in above example
Q3 (75th percentile): Q3 is the median of the upper half, again including the median of the entire data set. 50 is Q3 in above example

The inclusive method is often used in descriptive statistics and when dealing with smaller data sets, as it provides a more comprehensive view of the data distribution by including the central value in the calculation of quartiles.

Using Statistical Software (R, Python)

For those who work with large datasets or prefer programming, statistical software like R or Python offers powerful tools for calculating the IQR.

In R: #RStudio

data <- c(10, 15, 20, 35, 40, 45, 50, 55, 70)IQR(data)

In Python (using pandas): #Python

import pandas as pddata = pd.Series([10, 15, 20, 35, 40, 45, 50, 55, 70])IQR = data.quantile(0.75) - data.quantile(0.25)print(IQR)

Both methods will give you the IQR quickly, and they’re especially useful when handling large datasets where manual calculation is impractical.

Conclusion

The Interquartile Range is a vital tool in any statistician’s toolkit. It helps you understand the spread of your data, especially when outliers are present. Whether you’re calculating it manually, using spreadsheets, or employing software like R or Python, mastering the IQR will enhance your ability to analyze data effectively.
This comprehensive guide should arm you with everything you need to know about the IQR, making you well-prepared to tackle statistical challenges with confidence.

https://geekysteth.com/master-statistics-101-interquartile-range-iqr/

#science #StatisticsBasics

What is Correlation?

Correlation indicates that as one variable changes in value, the other variable tends to change in a specific direction. For example, the height and weight of an individual can be correlated – which means if the person’s height is on the taller side of the curve, the weight would also be high.

Table of Contents

What is Correlation?
What are correlation coefficients?
Pearson’s correlation coefficient
Correlation doesn’t imply causation.

What are correlation coefficients?

The correlation coefficient is a value that can quantitatively assess the strength and direction of the correlation or association between the two variables. One can choose different types of correlation coefficients depending on the type of data and the relationship you are looking at. One common correlation coefficient is the Pearson correlation coefficient, which explores the linear relationship between two continuous variables.

Pearson’s correlation coefficient

Before we proceed further, we need to learn how to interpret the correlation coefficient. Look at this by studying Pearson’s correlation coefficient (r)under the following subheadings.

Strength: The greater the absolute value of the correlation coefficient, the stronger the relationship between the variables. For example, -1 and 1 are the extremes in the range, indicating a linear relationship between the negative and positive variables, respectively. A coefficient of 0 indicates no correlation between the variables.
Direction: the sign of the correlation coefficient represents the direction of the relationship. For example, a negative sign indicates that the other variable’s value decreases as one variable’s value increases.
- One example of a negative correlation would be the engine’s horsepower and mileage per litre of gas or petrol. Engines with higher horsepower tend to consume more fuel, thus resulting in lower mileage per litre of gas or petrol.

Scatterplots are one of the best graphs to visualise and look for correlations between the variables. Here is an image of scatterplots featuring different Pearson’s correlation coefficients: -1, -0.5, 0, 0.5, 1

As you can see from the above graph, the stronger the correlation, the closer the data points are to the line, and the less the dispersion of the data points on the graph.

Pearson’s correlation coefficient measures only the linear relationship betwene the variables

If there is a curvilinear relationship between the variables, the person’s correlation coefficient might not detect it and might give you wrong, inaccurate values.

Correlation doesn’t imply causation.

You might have heard this rather infamous quote before: “Correlation doesn’t imply causation”. This is an important line to remember. Correlation doesn’t mean that changes in one variable will lead to changes in the value of the other variable.

So, if two variables are correlated, but there is no causal relationship, how can one explain the correlation between the two variables?
- A third variable might correlate with the other two variables, leading to the correlation between the first two variables. This third variable is called a confounder or confounding variable. This confounding variable correlates with the other two variables and creates confusion regarding which is a causal relationship and which is a spurious association. In statistics and trials, you need to perform a randomized controlled trial

Like this post? Share and subscribe to stay in the loop: Subscribe

https://geekysteth.com/master-statistics-101-correlation/

#correlation #math #StatisticsBasics