#DocMadhattan: The Abel Prize 2025: Masaki Kashiwara
https://docmadhattan.hashnode.dev/the-abel-prize-2025-masaki-kashiwara
Masaki Kashiwara wins the 2025 Abel Prize for groundbreaking work in algebraic analysis, D-modules theory, and crystal bases in representation theory
#mathematics #physics #AbelPrize #MasakiKashiwara #grouptheory #quantumgroups
I've kind of always wondered what the point of definitions like a group is a non-empty set \(G\) with a binary operation \(d\) satisfying \(d(d(d(z,d(x, d(x,x))),d(z,d(y,d(x,x)))),x) = y\) is, other than because we can, but https://math.stackexchange.com/a/4366021 offers one such answer in terms of homotopy type
searching for any structures / theory that involve a particular operation on non-empty lists of postitive integers like "the length of the list multiplied by the least common multiple of all the items in the list"
any ideas? references to any literature would be very appreciated if you know of any.
#askfedi #math #maths #mathematics #combinatorics #GroupTheory #DiscreteMath
Me: If you're a student in my class you will do group presentations, meaning that you will organize into a subset of the class, stand in front of the room, and talk about math to the rest of the class.
Also me: Let's talk about group presentations, a completely abstract algebraic concept that have absolutely nothing to do with standing in front of the room talking about your work.
Also also me: Okay, time for group presentations about group presentations.
#Algebra #ITeachMath #GroupTheory #GroupPresentation
Share via
existence of a single prototile that by itself forms an aperiodic set of prototiles; that is, a shape that can tessellate space but only in a nonperiodic way.
einstein problem can be seen as a natural extension of the second part of Hilbert's eighteenth problem, which asks for a single polyhedron that tiles Euclidean 3-space, but such that no tessellation by this polyhedron is isohedral.[3] Such anisohedral tiles were found by Karl Reinhardt in 1928, but these anisohedral tiles all tile space periodically.
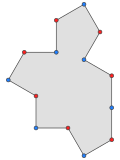
Partition of a plane in closed set - tile
2022, hobbyist David Smith discovered a "hat"-shaped tile formed from eight copies of a 60°–90°–120°–90° kite (deltoidal trihexagonals), glued edge-to-edge, which seemed to only tile the plane aperiodically.[8] Smith recruited help from mathematicians Craig S. Kaplan, Joseph Samuel Myers, and Chaim Goodman-Strauss, and in March 2023 the group posted a preprint proving that the hat, when considered with its mirror image, forms an aperiodic prototile set.[
Wiki
#grouptheory
What is a good website to teach Group Theory and Chemistry? #Chemistry #Mathematics #Spectroscopy #GroupTheory
New 📚 Release! Introduction to Group Theory: An Activity-Based Approach by Joe Fox #books #ebooks #math #grouptheory
This book is an introduction to group theory suitable for an introductory course in abstract algebra. Much of the content is delegated to a series of activities that are meant to be worked through by the students with the help of the instructor.
Find it on Leanpub!
Riffs and Rotes • Happy New Year 2025
• https://inquiryintoinquiry.com/2025/01/01/riffs-and-rotes-happy-new-year-2025/
\( \text{Let} ~ p_n = \text{the} ~ n^\text{th} ~ \text{prime}. \)
\( \text{Then} ~ 2025
= 81 \cdot 25
= 3^4 5^2 \)
\( = {p_2}^4 {p_3}^2
= {p_2}^{{p_1}^{p_1}} {p_3}^{p_1}
= {p_{p_1}}^{{p_1}^{p_1}} {p_{p_2}}^{p_1}
= {p_{p_1}}^{{p_1}^{p_1}} {p_{p_{p_1}}}^{p_1} \)
No information is lost by dropping the terminal 1s. Thus we may write the following form.
\[ 2025 = {p_p}^{p^p} {p_{p_p}}^p \]
The article linked below tells how forms of that sort correspond to a family of digraphs called “riffs” and a family of graphs called “rotes”. The riff and rote for 2025 are shown in the next two Figures.
Riff 2025
• https://inquiryintoinquiry.files.wordpress.com/2025/01/riff-2025.png
Rote 2025
• https://inquiryintoinquiry.files.wordpress.com/2025/01/rote-2025.png
Reference —
Riffs and Rotes
• https://oeis.org/wiki/Riffs_and_Rotes
#Arithmetic #Combinatorics #Computation #Factorization #GraphTheory #GroupTheory
#Logic #Mathematics #NumberTheory #Primes #Recursion #Representation #RiffsAndRotes
Want to formalize something in Mizar but don't know where to begin?
I'm starting a new series of posts with project ideas, starting with Loops! They're needed to formalize the sporadic groups (as found in, e.g., Aschbacher's book "Sporadic Groups").
I have been formalizing finite group theory in Mizar, and I am about to formalize representation theory.
So I thought I would write some "notes to myself" about it.
#proofassistant #grouptheory #RepresentationTheory #Mizar
https://thmprover.wordpress.com/2024/12/13/plans-for-representation-theory-in-mizar/
A shop called "Wreath Products" that sells mathematical puzzle toys, mobiles (like for baby cribs or art)...and, sure, also decorative wreaths.
It seems that most notation in finite group theory was chosen as an inside joke among a dozen people.
Example: Let B and Y be subgroups of X. The Cyrillic И_{Y}(B) denotes the set of B-invariant subgroups of Y --- i.e., the set of all subgroups of Y such that B normalizes it, i.e., \(\{H\leq Y\mid B\subset N_{Y}(H)\}\), because it's kinda like the mirror image of the normalizer. Get it? It's a reflected N, which we use for normalizers. Get it?
Funny, huh?
Sat Dec 7, 2024 on zoom & in-person
Session in memory of Richard Parker at the annual Nikolaus conference at Aachen (on group & representation theory). Main speakers:
Gerhard Hiß
Gabriele Nebe
Colva Roney-Dougal
This is honestly so cool. I love how kids toys and games can be the source of surprisingly complicated #math. In this case, using #groupTheory and #graphTheory to show how you can generate all possible configurations of a Rubik's cube without any repeats
https://bruce.cubing.net/ham333/rubikhamiltonexplanation.html
This textbook has heavy “demon summoning” vibes to it 😅
I have written a bit more about formalizing cosets of groups in Mizar.
Like other posts in my review of Group Theory in Mizar, this "walks through the thought process" underlying formalization of Mathematics.
#Mizar #GroupTheory #Math #proof #ProofAssistant
https://thmprover.wordpress.com/2024/10/28/cosets-of-groups-in-mizar/
[New Blog Post] Coset Enumeration using Equality Saturation https://www.philipzucker.com/coset_enum_egraph/ #egraph #grouptheory #algebra
A normal subpost is a subpost whose left and right coposts are equal.
#GroupTheory #SubPost
Finally read the famous paper on the GAP type system.
Actually an excellent read, at least for those interested in computational algebra and typesystems.
https://dl.acm.org/doi/10.1145/281508.281540
#algebra #computational #GAP #grouptheory #math #maths #types #typesystems
