#Braids #3StrandBraids

After we #sweepOneRail with the blue #sweepingCurve on the orange #railCurve for the #braid strand, we cap #planarHoles to get a single #airtight strand.

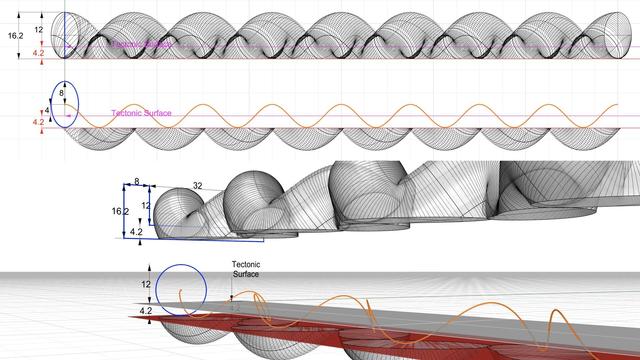
As described in https://pixelfed.social/p/Splines/798015349727305297, the radius of the blue circle is 8 units, and the total height of a strand swept by that circle is 24 units. Half of that is above the #tectonic surface, which is still twice of what #Vignola documented in #RegolaArchitettura.

We will apply #nonuniformScaling in the Z direction to reduce the height in half while keeping the length (X) and width (Y) the same. But before we do that we split and discard some of the bottom portion of the strand that is below the tectonic surface and is not needed.

The top half of the figure shows the front view of a single strand. The bottom shows the perspective view of the same strand.

Note that the orange braid rail starts at the center of the blue sweeping circle which looks like an ellipse in the front view. The orange rail itself looks like a flat sinusoid in the front view, but its beautiful meandering shape is really apparent in the perspective view.

The orange rail curve is centered on the "ground" or XY plane, which is also where the #tectonicSurface for the braid is. The amplitude of the orange curve (maximum or minimum from axis of the curve) is 4 units. We need to preserve the geometry of the strand at least up to the bottom of the orange rail.

If we split the strand exactly at 4 units below the ground plane, we hit a limit that not all #CAD tools are able to handle. To get around, we extend it past that limit by an arbitrarily small fraction, like 0.2, and discard the portions below. We could have extended it by 0.1 or 0.3 but it wouldn't have mattered.

Next, we draw a profile curve for the braid channel which is 32 units wide and its groove is 12 units tall for now. The rims on both sides of the channel are each 8 units wide. Total height of rim and channel is 16.2 units

#Braids #3StrandBraids

With the #rail curve for a #braid strand in https://pixelfed.social/p/Splines/797916882329430160, we can start the construction of a braid that matches the sketch in #Vignola's #RegolaArchitettura shown in https://pixelfed.social/p/Splines/793215298082967733.

The strands for this braid have a radius of 1 part or 8 units. So their diameter is 16 units, and the braid itself is 32 units wide.

To create one strand, we start with a circle of radius of 8 units perpendicular to the tip of the orange curve. We use the orange curve as a #railCurve and the blue circle as the #sweepingCurve in the #sweepOneRail operation.

Note that the circle appears distorted like an oval in all views — front view is on top-left, top view on top-right, right view in bottom-left, and perspective view in bottom-right. That is because the circle is perpendicular to the rail curve, not to any of the "world" coordinate planes. If the sweeping curve does not appear like an angled line in the top view, something is wrong.

After the sweep, close #planarHoles to get a solid strand and, as always, check for #nakedEdges and #nonManifoldEdges to ensure an #airtight object.

Refer again to the middle portion of the top diagram in https://pixelfed.social/p/Splines/793215298082967733 between the two bell shapes of the scrolls. The total width of the #tectonic surface on which the braid will be laid is 4 parts or 32 units wide. The braid has a rim 8 units wide on both sides that rises 6 units above the tectonic surface. Half of the braid should be above the tectonic surface, meaning that the total height of the braid should be 12 units.

If you check the bounding box of this strand, you find that it is indeed 32 units wide as needed, but the height is 24 units. So we have to apply #nonuniformScaling to keep X and Y scale intact but halve the scale in the Z direction. This will reduce the roundness of the strand and cut its height in half to 12 as needed.