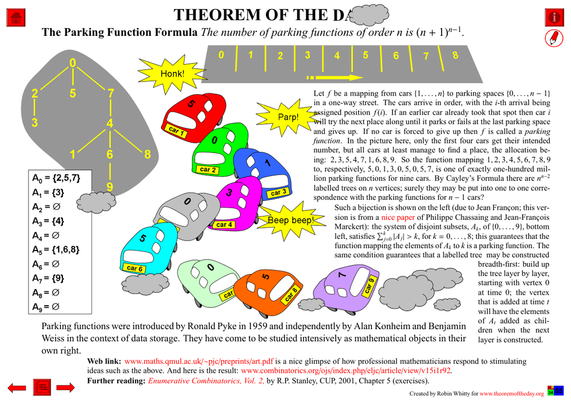
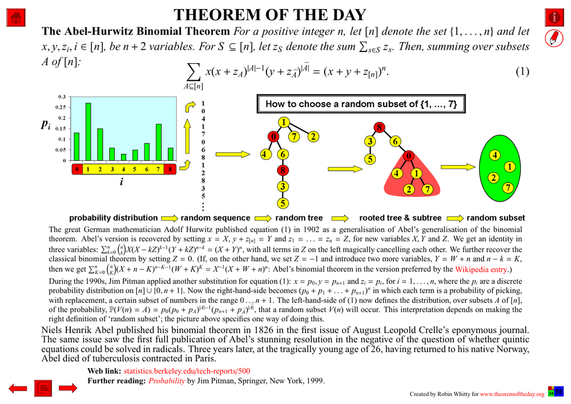
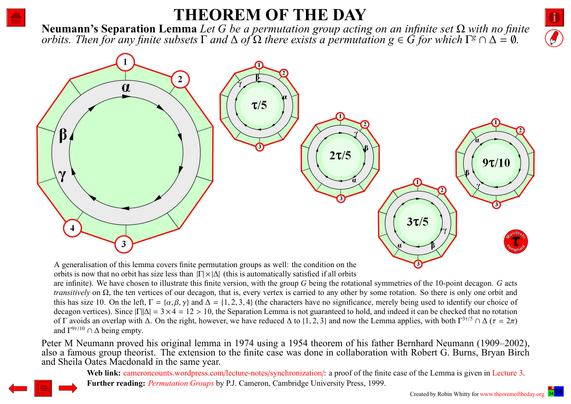
Now this animation is available for the 1000 sequences decomposed on my website.
Accessible from the 3Dgraph, 2Dgraph500terms and 2dgraphs pages ➡️ https://decompwlj.com
A little more work on axis sizing and controls.
#decompwlj #math #mathematics #maths #sequence #OEIS #JavaScript #php #graph #3D #threejs #webGL #triangular #numbers #primes #PrimeNumbers #palindromes #animation #FundamentalTheoremOfArithmetic #sequences #NumberTheory #classification #integer #decomposition #number #theory #equation #graphs #sieve #fundamental #theorem #arithmetic #research