How do I stop suspend mode from resetting my settings? #gnome #systemsettings #tiling
#tiling
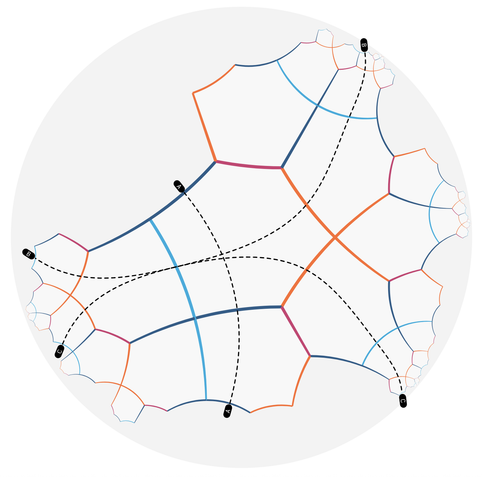
Advent of Tilings - Day 11.2
All the looping variants going through the central tile as defined by the two relators.
Advent of Tilings - Day 11.1
A genus 7 surface tiling with a bit more torsion.
Looping relators (f₁t₁)² and f₁f₂t₁t₂f₂
Advent of Tilings - Day 10.2
Again in the unwrapping it is possible to count the 48 tiles as in post “Day 9.1”.
Advent of Tilings - Day 10.1
Same number of same combinatorial tile, same number of tiles as yesterday, thus same genus, but a different way of glueing the boundary.
t₂² and (f₁t₁)³ are the glueing rules.
The immersion…
Advent of Tilings - Day 9.2
To immerse the tiling we wrap it up and dust a bit of geometry on it.
Advent of Tilings - Day 9.1
And now for something completely finite. Let’s have a look at some glittering genus 7 specimens.
They are made up of 48 of our hexagons. The stretched 48 tiles can be layed out in the Poincaré plane as always, along with the simple looping rules:
(t₂)³ and (f₁f₂)²
Feel free to count.
About a year ago I picked up a copy of Grünbaum and Shephard's "Tilings and Patterns" and was inspired to write a little #tiling generator in #rust . I had intended to build it into a bigger project but that bigger project never saw the light of day. Recently I decided to dust off that generator and enhance it a bit more for a new project that... is also kind of dubious as to whether it will ever see the light of day. But in the meantime the tiling generator itself can now make some pretty gifs!
(The tiling shown is a small patch of the Archimedean tiling 3.4.6.4, where the numbers in that notation indicate the polygons each vertex touches.) #indiedev #math
Advent of Tilings - Day 8.2
In the unfolded tiling embedded in the Poincaré plane you see the two looping relators in all the variations for the central tile:
t₂⁴ - t₂ edges are NAVY, see A-A
(f₁t₁t₁)² - f₁ edges are CYAN, t₁ edges are KAKI colored, see B-B, C-C and D-D
Advent of Tilings - Day 8.1
If we remove one looping relator from the day 7 cookie recipe, we get infinity, a monohedral tiling and perfect embedability in euclidian space.
t₂⁴ and (f₁t₁t₁)² but (f₁f₂f₁f₂f₁t₁⁻¹f₁t₁)² is removed
Advent of Tilings - Day 7
Chunky multilayered cookie held together by the rules
t₂⁴ and (f₁f₂f₁f₂f₁t₁⁻¹f₁t₁)² and (f₁t₁t₁)²
Non-monohedral and self-intersecting.
Advent of Tilings - Day 6.2
In the image below the t₂² relator is indicated with the markings A-A, and hints at why the tiling becomes flat when glued up.
Advent of Tilings - Day 6.1
For day 6 of hexagonal tilings we go flat and use the looping relators:
(f₁f₂)⁴ and t₂²
to create a tiling that is not embeddable in euclidian space, but can be monohedrally immersed with intersections of the tiles.
Advent of Tilings - Day 5.2
The twist as seen in the stretched unfolding into the hyperbolic plane.
Advent of Tilings - Day 5.1
This two periodic hexagonal tiling is a bit more twisted than the one from yesterday. Can you spot the difference between the rules?
t₂⁴ and (f₁f₂)²
Still embeddable in euclidian space and monohedral though.
Advent of Tilings - Day 4.2
… remember we are still basing the tiling off of the basic glueing group describing the tiling of the hyperbolic plane:
G = ⟨ f₁, f₂, t₁, t₂ | f₁², f₂², t₁⁴, f₂t₁⁻¹t₂⁻¹, (f₁t₂)² ⟩
And we just add the further looping relators to form the tiling of the surface with planar growth.
𝐚 = t₂⁴
𝐛 = (f₁t₁)²
H = ⟨ f₁, f₂, t₁, t₂ | f₁², f₂², t₁⁴, f₂t₁⁻¹t₂⁻¹, (f₁t₂)², 𝐚, 𝐛 ⟩
Here unfolded with the glueing rules spawned by the relators going through the central tile.
Advent of Tilings - Day 4.1
Why stay with the sugar canes when you can get waffles. Not only linear growth is possible, but also planar growth with just two looping rules.
t₂⁴ and (f₁t₁)²
And this time the tiling is embeddable in euclidian space and monohedral...
RE: https://toot.community/@openculture/115653657967404933
In some abstract way this reminds me of the graphical work of M.C. Escher.
Client Info
Server: https://mastodon.social
Version: 2025.07
Repository: https://github.com/cyevgeniy/lmst