Lmst

I've installed the mathlib docs, but it's not a copy of its online version. I got only warningsbut no errors, and references are disabled by default for some reason. Well, it's only an alternate if my ISP is having a bad connection day. #mathlib #docs #lean #nomxd #Tech-talk🐾

To run Mathlib, I had to install Elan. It installs whatever Lean version Mathlib (or some package) needs. Doing it without Elan is a pain (I've tried), so we begin removing our installation of Lean. #lean #mathlib #elan #lake #MV #新曲公開 #オリジナル曲 #newmusic #Tech-talk🐾

Readings shared May 10, 2025. https://jaalonso.github.io/vestigium/posts/2025/05/10-readings_shared_05-10-25 #ITP #LeanProver #Math #Mathlib #Python

LeanExplore: a new Mathlib search engine that combines semantic search embeddings, AI-generated translations, and PageRank to give optimized search results. https://www.leanexplore.com/ #ITP #LeanProver #Mathlib

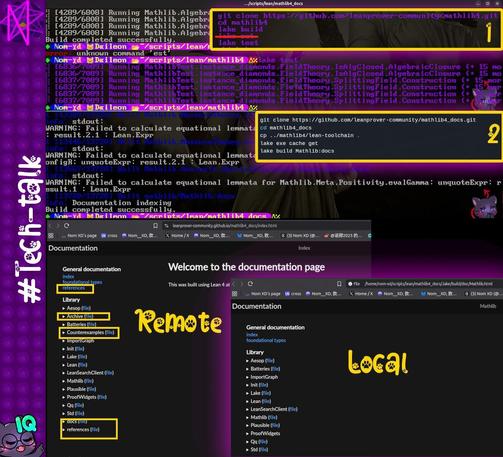
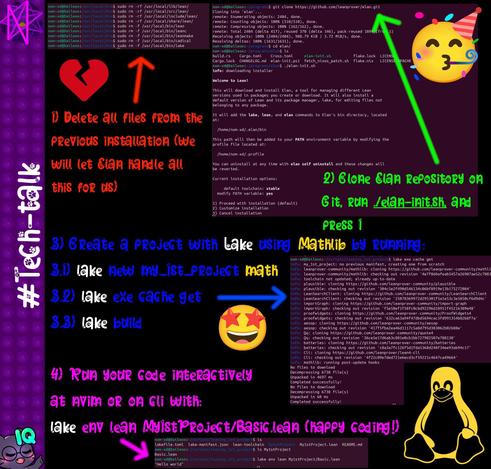
#mathlib has a fascinating set of counterexamples, which includes, for example, a disproof of the Aharoni–Korman conjecture: https://leanprover-community.github.io/mathlib4_docs/Counterexamples/AharoniKorman.html

when i'm in a #lean4 phase, i often think of (much, much more trivial) false statements, so i decided to just start proving that they were indeed false: https://g.pyrope.net/simple-counterexamples

the pace of additions will be somewhat rapid because the proofs are only a couple of lines at most. they're fun to think about, though—how would you prove that (haskell syntax) Monad m => m a -> a is inconsistent?

Readings shared April 2, 2025. https://jaalonso.github.io/vestigium/posts/2025/04/02-readings_shared_04-02-25 #FunctionalProgramming #HOL4 #Haskell #ITP #IsabelleHOL #LLMs #LeanProver #Logic #LogicProgramming #Math #Mathlib #Prolog

Basic probability in Mathlib. ~ Rémy Degenne. https://leanprover-community.github.io/blog/posts/basic-probability-in-mathlib/ #ITP #LeanProver #Mathlib #Math

" 𝗠𝗮𝘁𝗵𝘀 𝗣𝗿𝗼𝗼𝗳𝘀 𝗶𝗻 𝗟𝗲𝗮𝗻 - 𝗙𝗶𝗿𝘀𝘁 𝗦𝘁𝗲𝗽𝘀 " 🚀

Designed specifically for beginners struggling to get started with other courses and guides.

* Simple bite-sized examples.
* Focus on concepts, introduced gradually.
* One easy exercise per chapter.

.. all to build confidence, not demolish it !

https://www.amazon.com/dp/B0DWHS1RDJ

#maths #lean #mathlib #lean4

... it's out ! 🚀

" Maths Proofs in Lean - First Steps "

Designed specifically for newcomers and beginners struggling to get started with other courses and guides.

* Simple bite-sized examples explained.
* Concepts introduced gradually.
* One easy exercise per chapter.

.. all to build confidence, not demolish it !

https://www.amazon.com/dp/B0DWHS1RDJ

#maths #lean #mathlib #lean4

book cover: Maths Proofs in Lean First Steps

Readings shared February 5, 2025. https://jaalonso.github.io/vestigium/posts/2025/02/05-readings_shared_02-05-25 #ITP #IsabelleHOL #LeanProver #Mathlib #LLMs #Math

A semantic search engine for Mathlib4. ~ Guoxiong Gao, Haocheng Ju, Jiedong Jiang, Zihan Qin, Bin Dong. https://arxiv.org/abs/2403.13310 #ITP #LeanProver #Mathlib

As a step towards computer-formalizing the classification of low-dimensional Lie algebras, we finally formalized our first non-boring theorem in #Lean4 !

If L is a 3-dimensional Lie algebra (over any field) with a one-dimensional commutator subalgebra which is contained in the center of L, then L is isomorphic to the 3D Heisenberg algebra - that is, it has a basis (𝑒₀, 𝑒₁, 𝑒₂) such that the bracket is determined by
[𝑒₁,𝑒₂]=𝑒₀,
[𝑒₀,𝑒₁]=0,
[𝑒₀,𝑒₂]=0.

Now we're working on the analogous results for higher dimensional commutator subalgebras. These are going to be harder because
a) there's no one-size-fits-all classification statement for arbitrary fields, and
b) they rely on certain normal forms of matrices which aren't yet implemented in #mathlib .

The Matrix Cookbook, using Lean's mathlib. ~ Eric Wieser. https://github.com/eric-wieser/lean-matrix-cookbook #ITP #LeanProver #Lean4 #Mathlib #Math