Сумма из 51 узбекистанского сузани разных веков (выглядит как суммарное изображение из ковров). #summation #pictorialsummation #suzani #Uzbekistaniart #blurred #decorativeart #collage #publicdomain

@zvavybir
It does diverge. It has no sum.
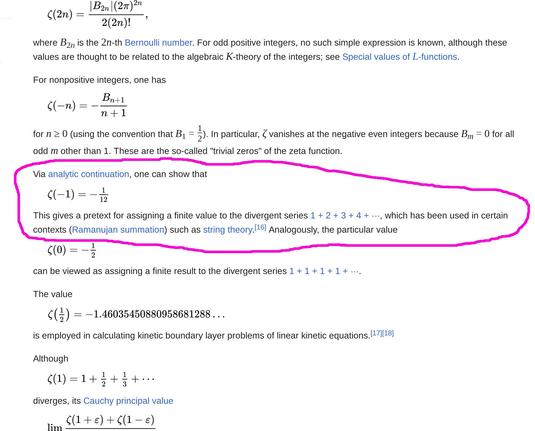
However, the uniquely valued #Riemann #ZetaFunction can be analytically continued into the left half-plane where we find zeta(-1)=-1/12 (which 'looks like' 1+2+...). #Cesàro #summation will get you part of the way there also, and, as you say, yields the same result; presumably due to some ultimate cosmic logical rightness :-)
I very strongly recommend BP's superb exposition of this issue
https://www.youtube.com/watch?v=YuIIjLr6vUA
#maths #AnalyticContinuation #Ramanujan

Try to prove the following two results that relate the harmonic numbers to the golden ratio. Have an excellent weekend.

\[\displaystyle\sum_{n=1}^\infty\binom{2n}n\dfrac{H_n}{5^n}=2\sqrt5\ln\varphi\]

\[\displaystyle\sum_{n=1}^\infty\binom{2n}n\dfrac{H_n}{5^nn}=\frac{2\pi^2}{15}-2\ln^2\varphi\]

where \(\varphi=\frac{1+\sqrt5}2\) is the golden ratio; and \(H_n=\left(1+\frac12+\frac13+\ldots+\frac1n\right)\) is the \(n\)-th harmonic number.

#GoldenRatio #HarmonicNumbers #HarmonicNumber #Logarithm #Pi #Summation #Math #Sum #InfiniteSum #Binomial #BinomialCoefficient #Maths #WeekendChallenge