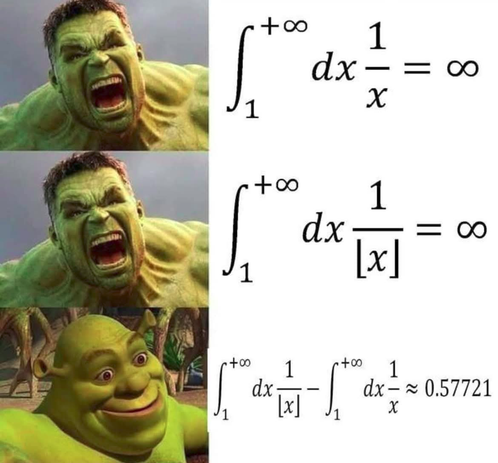Euler–Mascheroni constant! :euler:

In fact, the last one is:
\[\large\displaystyle\int_1^{+\infty}\mathrm dx\ \left(\frac{1}{\lfloor x\rfloor}-\frac1x\right)=\gamma\approx0.5772156649\]

Equivalently,
\[\large\displaystyle\lim_{n\to\infty}\left(\sum_{k=1}^n \frac1{k}-\ln n\right)=\gamma=0.5772156649\ldots\]
---------------------------------------------------------------------------------------------------------------------
Unsolved problem in mathematics:
Is Euler–Mascheroni constant irrational? If so, is it transcendental?

#Euler #Mascheroni #EulerMascheroni #Constant #gamma #EulerConstant #EulersConstant #EulerMascheroniConstant #Irrational #Irrationality #Transcendental #Transcendence #Unsolved #UnsolvedProblem #Maths #Mathematics #Indeterminate #IndeterminateForm #IndeterminateForms #Inf #Infinity #HarmonicNumber #HarmonicNumbers #HarmonicSeries #Logarithm #Log #Logarithms #NaturalLogarithm #Integral #ImproperIntegral

Try to prove the following two results that relate the harmonic numbers to the golden ratio. Have an excellent weekend.

\[\displaystyle\sum_{n=1}^\infty\binom{2n}n\dfrac{H_n}{5^n}=2\sqrt5\ln\varphi\]

\[\displaystyle\sum_{n=1}^\infty\binom{2n}n\dfrac{H_n}{5^nn}=\frac{2\pi^2}{15}-2\ln^2\varphi\]

where \(\varphi=\frac{1+\sqrt5}2\) is the golden ratio; and \(H_n=\left(1+\frac12+\frac13+\ldots+\frac1n\right)\) is the \(n\)-th harmonic number.

#GoldenRatio #HarmonicNumbers #HarmonicNumber #Logarithm #Pi #Summation #Math #Sum #InfiniteSum #Binomial #BinomialCoefficient #Maths #WeekendChallenge

A representation of \(18\) using an analytic continuation of the Dirichlet series and the numbers \(0, 1,2,3,4,5,6\).
\[18=\left|\dfrac{1}{\zeta^2(0)}\left(\dfrac{\mathcal{H}(-6)}{\zeta(-5)}-\dfrac{\mathcal{H}(-2)}{\zeta(-1)}\right)\dfrac{\mathcal{H}(-4)}{\zeta(-3)}\right|\]
where \(\displaystyle\zeta(z)=\sum_{n\geq1}\dfrac{1}{n^z}\) denotes the Riemann zeta function, and \(\displaystyle\mathcal{H}(z)=\sum_{n\geq1}\dfrac{H_n}{n^z}\) denotes the harmonic zeta function.

#ZetaFunction #RiemannZetaFunction #HarmonicZetaFunction #AnalyticContinuation #DirichletSeries #Series #Numbers #Zeta #Harmonic #HarmonicNumbers #Representation #Function #Expression