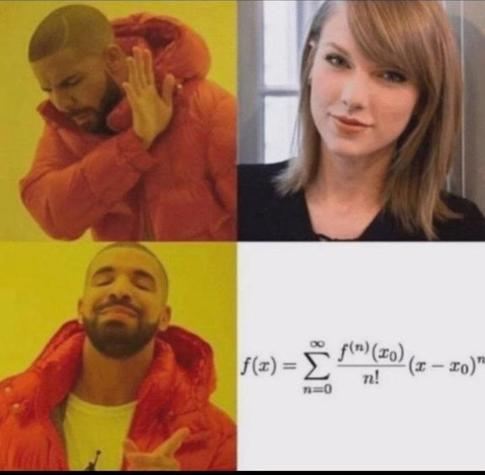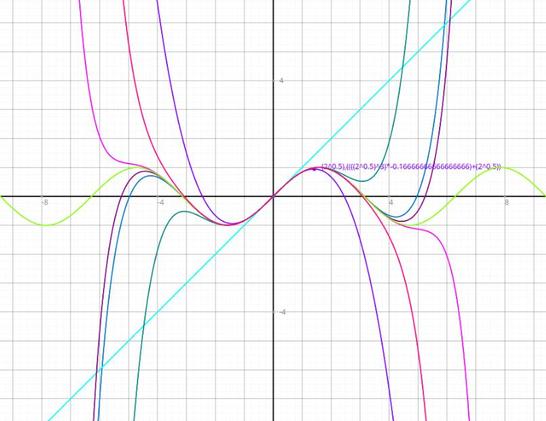
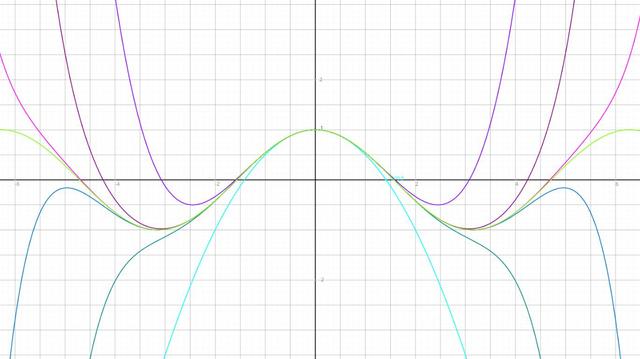
Day 24 of ‪Ayliean's @ayliean.bsky.social‬ #MathArtMarch thread Two pairs of #equal #equations: y=sin(x) equals y=x-x³/3!+x⁵/5!-...+x^(2n-1)/(2n-1)! y=cos(x) equals y=1-x²/2!+x⁴-...+x^(2n)/2n! See ALT, please! #mathematics #trigonometry #sine #cosine #Taylorseries #Taylorexpansion #Euleridentity

RE: https://bsky.app/profile/did:plc:enw4w6ihzt4uomkphuxuvczu/post/3lje6cgmacs2u

And yes, I went to her concert and actually wrote that formula down on the notes I had.
#taylorswift #taylorseries #memes #meme #irl

“How Does A Computer/Calculator Compute Logarithms?”, Zach Artrand (https://zachartrand.github.io/SoME-3-Living/).

Via HN: https://news.ycombinator.com/item?id=40749670 (which provides important addenda)

#Calculator #Mathematics #Maths #Logarithms #TaylorSeries #NumericalMethods #NumericalAnalysis #FastMath

https://martincmartin.com/2024/06/14/how-i-found-a-55-year-old-bug-in-the-first-lunar-lander-game/

#LunarLander #SoftwareBug #RetroGaming #Programming #TaylorSeries

LAGRANGE-BÜRMANN THEOREM
Have you heard about the Lagrange-Bürmann formula? It gives the Taylor series expansion for the inverse of a function.

If \(z=f(\omega)\) with \(f\) analytic at a point \(a\) and \(f(a)\neq0\), then
\[\omega=g(z)=a+\displaystyle\sum_{n=1}^\infty g_n\dfrac{(z-f(a))^n}{n!}\]
\[\text{where }g_n=\displaystyle\lim_{\omega\to a}\left[\dfrac{\mathrm{d}^{n-1}}{d\omega^{n-1}}\left(\dfrac{\omega-a}{f(\omega)-f(a)}\right)^n\right]\]

#Lagrange #Burmann #LagrangeBurmannTheorem #TaylorSeries #InverseFunction #Mathematics #Math #Maths

Kaze Emanuar’s Adventures in Mario 64 Optimization: Calculating Sine
I've mentioned Kaze Emanuar's efforts to make the best Mario 64 there can possibly be on its native hardware. He's compiled it with optimization flags turne
https://setsideb.com/kaze-emanuars-adventures-in-mario-64-optimization-calculating-sine/
#development #niche #retro #cosine #development #kazeemanuar #mario #mario64 #math #n64 #niche #nintendo #optimization #retro #sine #taylorseries #trigonometry #video #youtube

FOURIER SERIES AND TAYLOR SERIES

#FourierSeries #TaylorSeries #TaylorExpansion

The Fourier Series and the Taylor Series have something in common. Each of them arose with this train of thought: "Let's assume I can represent a given function by the sum of terms of a given type [polynomials with Taylor, sines/cosines with Fourier]. The only question is how to weight those terms properly. How, HOW can I possibly torture my function to get it to confess the appropriate weight of each term?"

In the case of Taylor, you can torture your function by taking its derivative: to get a given polynomial term's weight, you take the derivative of the function however many times, so that it's coughed up a term that is just a constant. Then that constant becomes the weight of that polynomial term. Do that for all the polynomial terms and you get all the polynomial term weights, and that lets you construct a complete representation of your original function out of polynomial terms.

In the case of Fourier, the form of torture is different. If you look at sin(x), sin(2x), sin(3x), etc, you'll notice that they all repeat every 2*pi (and in fact most of them will repeat more than once every 2*pi, but the important thing is, they all happen to line up with that 2*pi). Now, one interesting property of the integral from 0 to 2*pi is, if your integrand is the product of any pair of those sine terms, the integral evaluates to zero ... BUT if it's a term times itself, the integral is non-zero. That can be the our instrument of torture: you can, for example, take the integral of sin(3x)*f(x) to get f(x) to confess how much sin(3x) it contains, and that will tell us how to weight sin(3x).

#trigonometry #numericalmethods #taylorexpansion #taylorseries

So a YouTube video got me thinking about numerical methods for calculating sines and cosines. Not that it's important for most purposes, because essentially every programming language and math-capable utility has built-in sine and cosine functions.

Nevertheless, if you wanted to write the code yourself, you would at some point be doing a Taylor Expansion for sine and cosine according to the usual formulas. The problem is getting the expansions to converge to accurate, reliable values in as few terms as possible. Here is what I would recommend:

1) Angles greater than pi or less than -pi, add or subtract multiples of 2*pi to bring them between -pi and pi.

2) Use symmetry to map the angle to the range 0 to pi/2.

3) Angles from pi/4 to pi/2, you can calculate as the complementary function on the complementary angle. In other words, if you want to figure out the sine of 85 degrees, you can instead calculate the cosine of 5 degrees. So that reduces all our calculations to angles from 0 to pi/4.

All of that is obvious. Here's the part that is less obvious:

4) Figure out the sine and cosine of angles 0, pi/16, pi/8, 3*pi/16, and pi/4. As in, pre-calculate them, and store them as constants in your program. Now remember these trig identities:

sin(a+b) = sina*cosb + cosa*sinb

cos(a+b) = cosa*cosb - sina*sinb

Those identities will let you calculate all your angles as offsets from 0, pi/16, pi/8, 3*pi/16, or pi/4, whichever is closest. Like, suppose you wanted to calculate sin(7*pi/64). Well, think of that as sin(pi/8 - pi/64). Based on the trig identities above, that'd be sin(pi/8)*cos(pi/64) - cos(pi/8)*sin(pi/64). And remember, we have the sine and cosine of pi/8 pre-calculated, so all that's left is doing the Taylor Expansions on cos(pi/64) and sin(pi/64), which will resolve in only a few terms.

You could take this thinking further, where you're doing offsets against multiples of pi/32 or even pi/64. Whatever lets you get an accurate result in only a handful of expansion terms

Doing some preliminary organization work for my #Calculus II class in the Spring. I never heard about this guy, who is claimed to have known #pi to 11 digits and to have forshadowed #TaylorSeries about a a few centuries before #Newton.

https://en.wikipedia.org/wiki/Madhava_of_Sangamagrama

@charlottekl

The first thing that happens is a doubling of variables, roughly akin to position variables and first order differentials of position variables. Stuff analogous to #Gradients, #TangentFunctors, #TaylorSeries follows but I haven't got as far as genuine dynamics, more like simple kinematics. At any rate I'll be following your #Tootorial with interest to see what I can see analogy-wise on the lower road I'm pursuing. Regards, Jon

#xkcd: #TaylorSeries

https://xkcd.com/2605/