I an in Glasgow for the Leslie Fox prize meeting, celebrating young people's contributions to numerical analysis. Already heard two interesting talks. I velieve four more are to follow. Exciting!
#NumericalAnalysis
Whoa, hold onto your protractors! 🤓 Rohan's blog post just made Gaussian integration the hip new thing for the cool kids of numerical analysis. Because nothing screams "party" like Chebyshev-Gauss quadrature and evaluating definite integrals! 🎉
https://rohangautam.github.io/blog/chebyshev_gauss/ #GaussianIntegration #ChebyshevGauss #NumericalAnalysis #MathIsCool #PartyWithMath #HackerNews #ngated
Gaussian Integration Is Cool
https://rohangautam.github.io/blog/chebyshev_gauss/
#HackerNews #Gaussian #Integration #Cool #Mathematics #Algorithms #NumericalAnalysis
New publication https://doi.org/10.1103/PhysRevB.111.205143
New algorithm for the #inverseproblem of Kohn-Sham #densityfunctionaltheory (#dft), i.e. to find the #potential from the #density.
Outcome of a fun collaboration of @herbst with the group of Andre Laestadius at #oslomet to derive first mathematical error bounds for this problem
#condensedmatter #planewave #numericalanalysis #convexanalysis #dftk
That first implementation didn't even support the multi-GPU and multi-node features of #GPUSPH (could only run on a single GPU), but it paved the way for the full version, that took advantage of the whole infrastructure of GPUSPH in multiple ways.
First of all, we didn't have to worry about how to encode the matrix and its sparseness, because we could compute the coefficients on the fly, and operate with the same neighbors list transversal logic that was used in the rest of the code; this allowed us to minimize memory use and increase code reuse.
Secondly, we gained control on the accuracy of intermediate operations, allowing us to use compensating sums wherever needed.
Thirdly, we could leverage the multi-GPU and multi-node capabilities already present in GPUSPH to distribute computations across all available devices.
And last but not least, we actually found ways to improve the classic #CG and #BiCGSTAB linear solving algorithms to achieve excellent accuracy and convergence even without preconditioners, while making the algorithms themselves more parallel-friendly:
https://doi.org/10.1016/j.jcp.2022.111413
4/n
People in the market for a postdoc position in numerical linear algebra should look at the advert for a postdoc in Edinburgh "devoted to research on Randomized Numerical Linear Algebra for Optimization and Control of Partial Differential Equations."
The mentors are John Pearson (Edinburgh) and Stefan Güttel (Manchester), both excellent people, and the topic is fascinating. I even fantasised about leaving my permanent job and doing this instead ...
More info: https://www.jobs.ac.uk/job/DNA984/postdoctoral-research-associate
#NumericalAnalysis #optimization #PartialDifferentialEquations #postdoc
Thanks to the Manchester NA group for organizing a seminar by David Watkins, one of the foremost experts on matrix eigenvalue algorithms. I find numerical linear algebra talks often too technical, but I could follow David's talk quite well even though I did not get everything, so thanks for that.
David spoke about the standard eigenvalue algorithm, which is normally called the QR-algorithm. He does not like that name because the QR-decomposition is not actually important in practice and he calls it the Francis algorithm (after John Francis, who developed it). It is better to think of the algorithm as an iterative process which reduces the matrix to triangular form in the limit.
SUperman: Efficient Permanent Computation on GPUs
Ten Digit Problems (2011) [pdf] — https://people.maths.ox.ac.uk/trefethen/publication/PDF/2011_137.pdf
#HackerNews #TenDigitProblems #PDF #Mathematics #Research #NumericalAnalysis
Apparenty we weren't having enough issues of context collapse for #SPH as an acronym of #SmoothedParticleHydrodynamics, since I'm now seeing #STI as an acronym for #SymplecticTimeIntegrator. And of course these article are more often than not written with #LaTeX.
(No, Mastodon, I really do not want you to normalize the case of *that* tag.)
One of these I'm going to create a quiz game: #kink #fetish or #numericalAnalysis?
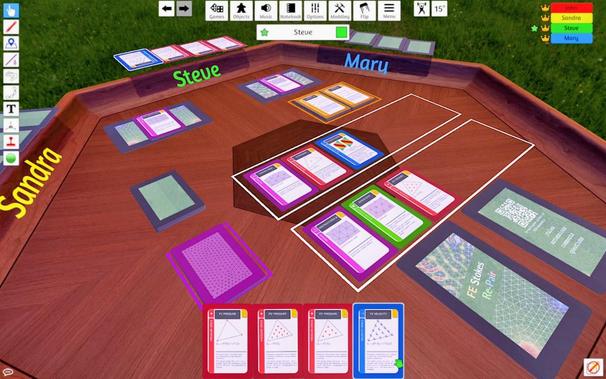
✨ A small dream came true last year: In the past year, we developed our very own (nerd) card game: FEStokes-RePair! 🎉🃏
The game uses the finite element discretization of the Stokes equations as a metaphor.
For details see here: https://fe-nerd-games.github.io/FEStokesRePair/ (and the following thread)
#NumericalAnalysis
#MathGames
#EducationalGames
#FiniteElements
#FEStokes-RePair
I am grateful to the London Mathematical Society and the Heilbronn Institute for Mathematical Research for their support in the creation of a Numerical Analysis network (named not very creatively NaN) in the north of UK. The network encompasses the universities of Manchester, Strathclyde, Edinburgh and Leeds.
We are now trying to organize a one-day workshop in Manchester in January.
#NumericalAnalysis #LondonMathematicalSociety #HeilbronnInstitute #ManchesterUniversity
Testing GPU Numerics: Finding Numerical Differences Between NVIDIA and AMD GPUs
I am excited to read about numpy_quaddtype, a project to include quad precision in numpy. The standard precision in numpy (and most other places) is double precision: numbers are stored in 64 bits and the precision is about 16 decimal digits. This is usually enough but not always.
Numpy does have longdouble, which may or may not increase precision, depending on your platform, but even if it does, the increase is very modest. If I need more precision, I typically use FLINT, but that is meant for super high precision and rigorous computations. It will be very good to have another tool.
More details in this blogpost: https://labs.quansight.org/blog/numpy-quaddtype-blog
I recently read two interesting survey articles by my academic brother Ben Adcock at Simon Fraser University about theoretical aspect of sampling: how to approximate a function 𝑓 given random point samples 𝑓(𝑥ᵢ) with noise. This is a fundamental problem in Machine Learning.
The first paper, "Learning smooth functions in high dimensions: from sparse polynomials to deep neural networks" (by Ben and co-authors), is about how fast the approximation error may decrease as you take more samples. We can overcome the curse of dimensionality if the function gets increasingly smooth in higher dimensions. URL: https://arxiv.org/abs/2404.03761
The second paper, "Optimal sampling for least-squares approximation", is about choosing where to sample in order to get as close to the unknown function (in least-square sense) as possible. https://arxiv.org/abs/2409.02342
Anyone here know anything about global optimization using interval analysis? #numericalanalysis
Book review: Beautiful Code edited by Andy Oram and Greg Wilson https://ianhopkinson.org.uk/2024/08/book-review-beautiful-code-edited-by-andy-oram-greg-wilson/ #softwaredevelopment #code #python #numericalanalysis #bookreview #bookstodon
I learned so much during my PhD, compared with the 15 years afterwards. Yesterday I did some light research on the theory of Runge–Kutta methods, which I learned during my PhD. And then, in a discussion with a colleague about a student's summer project, I could make a connection with the Euler–Maclaurin formula which I learned about during my PhD.
“How Does A Computer/Calculator Compute Logarithms?”, Zach Artrand (https://zachartrand.github.io/SoME-3-Living/).
Via HN: https://news.ycombinator.com/item?id=40749670 (which provides important addenda)
#Calculator #Mathematics #Maths #Logarithms #TaylorSeries #NumericalMethods #NumericalAnalysis #FastMath