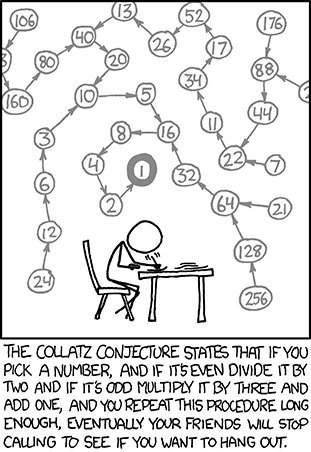
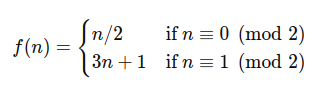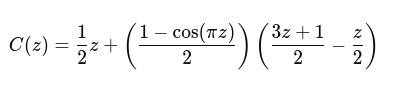🚿✨ So, after soaking in the shower like Archimedes, someone "visualized" the Collatz Conjecture in a way that the world was *definitely* waiting for. 🧼💡 Maybe next we'll hear about their groundbreaking #insights on shampoo bottles? 🤷‍♂️
https://abstractnonsense.com/collatz/ #CollatzConjecture #ShowerThoughts #Visualization #ShampooBottles #HackerNews #ngated

I asked ChatGPT to extend the Collatz Conjecture to the complex plane (and it made sense)

I was at a loose end, so I thought I would see if ChatGPT could extend Collatz into complex numbers. This was the reply.

Extending the Collatz Conjecture to the complex plane is a fascinating idea, though it leads into uncharted and nontrivial mathematical territory. Here’s a breakdown of the options and some of the considerations involved:

🔢 Original Collatz: Defined on ℕ

The original Collatz function is a piecewise function on the positive integers:

This is based on parity (odd or even), which doesn’t naturally extend to the complex plane ℂ.

🧩 Challenges in Extending to ℂ

To generalize to complex numbers, we must:

1. Replace parity-based rules with something continuous or analytically defined.
2. Define a continuous analogue or complex dynamical system resembling Collatz behavior.

🧮 Option 1: Complex Analogue Using Modular Extension

One approach is to construct an analytic function that smoothly interpolates between the two piecewise rules.

Lagarias & Weiss (1992) considered functions like:

I was surprised that ChatGPT cited a real paper.

This simplifies to:

I’d hardly claim this was much of a simplification.

Which behaves like:

Thus, this function smoothly mimics the parity behavior of integers, but it is now defined for all complex numbers.

🎨 Option 2: Visualizing Collatz-like Dynamics in ℂ

Instead of defining a “true” complex Collatz, some researchers explore dynamical systems that generalize the iterative structure:

• Iterate a function

• Use color plots or escape-time plots (similar to Mandelbrot sets) to visualize the behavior.

⚙️ Option 3: Integer Sequence Extended to ℂ Numerically

Alternatively, you could treat the original Collatz steps as a discrete complex function:

This would define a heuristic parity rule based on the real part of zzz, though it’s less elegant and doesn’t retain the analytic properties you’d want for complex dynamics.

Summary

to interpolate Collatz behavior

NGL, some of that was lost on me. So I asked Chat to explain the Complex Analogue Using Modular Extension like I was a GCSE student.

That kinda makes sense. I might write some bad Python and play with this. (later)

#ChatGPT #CollatzConjecture #complexPlane

#XKCD #CollatzConjecture #maths #mathematics #BusyBeaver

Collatz's Ant

https://gbragafibra.github.io/2025/01/08/collatz_ant2.html

#HackerNews #Collatz #Ant #CollatzConjecture #MathProblems #Algorithms #HackerNews

Ah, the esteemed Collatz Conjecture! 🎩 A mathematical riddle so perplexing that geniuses have resorted to fixed point theorems in metric spaces to solve it. 🚀 But let's be honest, reading this paper feels like being trapped in a Möbius strip of jargon—you're just going in circles! 😅🔄
https://arxiv.org/abs/2502.20642 #CollatzConjecture #MathRiddles #FixedPointTheorems #MöbiusStrip #GeniusProblems #HackerNews #ngated

A Proof of the Collatz Conjecture

https://arxiv.org/abs/2502.20642

#HackerNews #CollatzConjecture #Mathematics #Proof #NumberTheory #Research

Collatzeral Damage: Bitwise and Proof Foolish

Let’s talk about the Collatz Conjecture, which is like mathematicians’ original version of this programmer joke:

The Collatz conjecture is an infamous trap for the young and ambitious. Despite its simple construction, it has evaded proofs and general solutions for nearly a century. Veritasium made a video about this conjecture, which I recommend:

https://www.youtube.com/watch?v=094y1Z2wpJg

The Collatz conjecture involves a recursive function that contains one branch: If a number is odd, multiply it by 3 then add 1. If it is even, divide it by 2.

The conjecture states that repeating this operation will eventually reach 1 for all positive integers.

Quick observation:

• Even numbers take you closer to your goal of reaching your goal (reaching 0).
• Odd numbers take you further away from your goal.

You can write recursive code that implements the Collatz function like so:

function collatz(num) {  console.log(num);  if (num === 1) {    return;  }  return (num % 2 === 1)     ? collatz((3 * num) + 1)    : collatz(num >> 1);}

If the Collatz conjecture is false, there is some integer for which the return statement will never be reached.

We don’t know if the conjecture is true or not.

We do know that it has held up for a hell of a lot of positive integers (from a human perspective), and have yet to find a counterexample, but we don’t know if it’s necessarily true for all positive integers.

What if there’s actually a cycle somewhere (similar to what I discussed in the context of hash functions)?

That mathematicians don’t know the answer isn’t really interesting for the readers of this blog, but why the answer is so elusive (despite the intuitive simple construction of the function central to the Collatz conjecture) is something I think we can say something interesting about.

But first, let’s talk about a class of cryptographic algorithm that serves as the building block for several types of hash functions and stream ciphers used across the Internet today.

Important

I am taking a lot of liberties in this blog post, and I am prioritizing clarity over technical precision.

Readers will be better served by cross-referencing this entertainment-focused blog post with the work of actual mathematicians.

And for the pedants in the audience: if something seems imprecise, it’s probably because I made a trade-off to help a wider audience gain a basic intuition.

Add, Rotate, XOR (ARX)

ARX is a category of cryptography algorithms that is used to build various cryptography building blocks. The SHA-2 family of hash functions and the ChaCha stream cipher both an ARX construction (and both are used in a lot of Internet traffic).

Let’s focus on ChaCha for the moment, focusing on the reference implementation that ships with libsodium:

#define U32C(v) (v##U)#define U32V(v) ((uint32_t)(v) &U32C(0xFFFFFFFF))#define ROTATE(v, c) (ROTL32(v, c))#define XOR(v, w) ((v) ^ (w))#define PLUS(v, w) (U32V((v) + (w)))#define PLUSONE(v) (PLUS((v), 1))#define QUARTERROUND(a, b, c, d) \    a = PLUS(a, b);              \    d = ROTATE(XOR(d, a), 16);   \    c = PLUS(c, d);              \    b = ROTATE(XOR(b, c), 12);   \    a = PLUS(a, b);              \    d = ROTATE(XOR(d, a), 8);    \    c = PLUS(c, d);              \    b = ROTATE(XOR(b, c), 7);

At the core of ChaCha is the quarter round function. This is applied on alternating columns and diagonals of the input state until the desired number of rounds has been completed.

for (i = 20; i > 0; i -= 2) {    QUARTERROUND(x0, x4, x8, x12)    QUARTERROUND(x1, x5, x9, x13)    QUARTERROUND(x2, x6, x10, x14)    QUARTERROUND(x3, x7, x11, x15)    QUARTERROUND(x0, x5, x10, x15)    QUARTERROUND(x1, x6, x11, x12)    QUARTERROUND(x2, x7, x8, x13)    QUARTERROUND(x3, x4, x9, x14)}

After all rounds are complete, the initial state is added to the output. This 512-bit state includes the key (which consists of up to 256 bits), nonce, and some constant values. Because half of the input bytes are your secret key, an attacker without knowledge of the key cannot invert the calculation.

ChaCha is an improvement of another stream cipher from the same family as the eSTREAM finalist, Salsa20. ChaCha improved the diffusion per round and performance. This makes ChaCha less susceptible to cryptanalysis, even in extremely reduced-round variants (e.g., ChaCha8 vs ChaCha20).

As interesting as all that is, the important bits to know is that the ChaCha update emphasized improving diffusion.

What does that mean, exactly?

What is Diffusion?

Diffusion is a measurement of how much the output state changes when each bit differs in the input state.

This is important for making it difficult to statistically analyze the relationship between the input and outputs of a cryptographic function.

ARX Diffusion

ARX consists of three operations: Rotation (sliding bits around like a flywheel), addition, and eXclusive OR (also known as XOR).

Comparing Salsa20 and ChaCha’s quarter round, using the notation from the source code on Wikipedia, you see:

Salsa20 Quarter Round

b ^= (a + d) <<<  7;c ^= (b + a) <<<  9;d ^= (c + b) <<< 13;a ^= (d + c) <<< 18;

Addition then rotation then XOR.

ChaCha Quarter Round

a += b; d ^= a; d <<<= 16;c += d; b ^= c; b <<<= 12;a += b; d ^= a; d <<<=  8;c += d; b ^= c; b <<<=  7;

Addition then XOR then rotation.

Each step of the quarter round function still involves addition, rotation, and XOR, but their usage is different. (Also, they just update values directly rather than involving an extra temporary value to implicitly occupy a stack register.)

And it’s subtle, but if you play with these different quarter rounds with slightly different inputs, you can see how the diffusion is improved with the second construction in fewer numbers of rounds.

“Why does diffusion matter?”

Bit diffusion in ARX constructions is one of the ways that ciphers ensure their output remains indistinguishable from a random oracle.

If you’ve ever looked at a cryptographic hash function before, or heard about the “avalanche effect“, that’s precisely what we want out of these ARX constructions.

“So what?”

As some of you might remember from your studies, XOR is just addition without carry (mod 2).

If you repeat your same experimentation but only use one operation (AR or RX), you’ll find that your diffusion is poor.

This is because addition is an abstraction that hides a very important feature that’s often taken for granted.

Carry Propagation

Let’s say, for a learning exercise, you wanted to build integer addition entirely out of bitwise operators: AND, OR, NOT, XOR, and the left and right bit shift operators.

As already mentioned above, XOR is just addition without carry. So that part’s easy:

def add_bits_no_carry(x, y):    return x ^ y

How about carrying values to the next place? Well, consider the following table:

That third column sure looks like an “AND” operator, does it not?

Great, but what if you had a carry value from the previous step?

Well, now you have to implement two half-adders: One to handle the input carry value with one input, and the other to handle the other input and produce the next output carry value.

def half_adder(x, y):    return [x ^ y, x & y]def add_bits(x, y, c_in):    [a, b] = half_adder(x, y)    [d, e] = half_adder(a, c_in)    return [d, b ^ e]

If you feel lost, this hardware tutorial explains it with diagrams.

The main thing I want you to take away is that addition is much more complicated than XOR because of carry propagation.

On Computation and Information Theory

We use XOR to mix data (which could be plaintext, or could be all zeroes) with pseudo-random bytes, since it’s perfectly hiding so long as the bytes we’re mixing them with is unknown. This is the intuition underlying one-time pads and modern stream ciphers (including the ones we’re discussing).

In the context of ARX, because some operations (addition) propagate carries and others don’t (XOR), when you combine these steps with rotating the bits in-place, it becomes very easy to mix the output bits in a short number of rounds of operations. Cryptographers measure how well bits are mixed across a large number of inputs and reject designs that don’t perform well (generally speaking).

But a direct consequence of the hidden complexity of addition with carry is that the state you’re operating within is larger than the output. This means that some information is used (carried over from previous bits or limbs) that is not revealed directly in the output bit(s).

It’s easy to add two numbers together, but if you don’t know either of the numbers, it’s impossible to know the other (unless, of course, a side-channel leaks enough information to deduce one of them).

“That’s neat and all, but what does it imply?”

Don’t worry, I’m going somewhere with this.

Turing the Page

Let’s briefly talk about Turing machines.

The relevant Wikipedia article covers them adequately well. For everyone else, another Veritasium video:

https://www.youtube.com/watch?v=HeQX2HjkcNo

A Turing machine is a mathematical model for computation.

The basic idea is that you have a tape of symbols, a head that reads from the tape, and an internal state that determines the next move.

We don’t need too formal of a treatment here. I’m not exactly trying to prove the halting problem is undecidable.

A dumb joke I like to tell my computer science friends:

I’ve solved the Halting problem! It’s called: “the heat death of the universe,” at which point the program fucking halts!

But do put a pin in this, because it will come up towards the end.

Bitwise Collatz Functions

Above, I wrote a bit of code that implements the Collatz function, but I was a bit lazy about it.

In truth, you don’t need multiplication or the modulo operator. You can, instead, use bitwise operations and one addition.

• The modulo 2 check can be replaced by a bitwise AND mask with 1. Odd values will return 1, even will return 0.
• When the least significant bit is 0:
  Dividing by 2 is the same as right-shifting by 1.
• When the least significant bit is 1:
  Multiplying by 3 then adding 1 can be rewritten as the following steps:
  • Left shift by 1 (2n)
  • Set the lower bit to 1 (+1), using bitwise OR
  • Add the original number (+n)

Thus, our function instead looks like:

function collatz(num) {  console.log(num);  if (num === 1) {    return;  }  return (num & 1)    ? collatz(((num << 1) | 1) + num)    : collatz(num >> 1);}

That is to say, you can implement most of the Collatz function with bitwise operators, and only need one addition (with carries) in the end.

Suddenly, the discussion above about carry propagation might seem a lot more relevant!

Small Example

Imagine you encode a number as a binary string. For example, 257.

When you work through the algorithm sketched out above, you end up doing this:

       n == 0001_0000_0001     2*n == 0010_0000_0010 # left shift by 1 2*n + 1 == 0010_0000_0011 # bitwise OR with 1       add: 0001_0000_0001 # n            0010_0000_0011 # 2n + 1            # This is where carry propagation comes in!    result: 0011_0000_0100

When you perform the 3n+1 branch of the Collatz function the way I constructed it, that last addition of n will propagate carries.

And that carry propagation is where the trouble starts.

Since the (3n+1) branch is only ever invoked with odd values for n, you can guarantee that the next step will be followed by at least one division by 2 (since 3n+1 is even for any odd n).

This allows you look ahead two steps at a time, but there is no easy way to predict how many back-to-back (3n+1)/2 two-steps you will encounter from a given value. Instead, you have to actually perform the calculation and see what happens.

Collatz Machines

The input and output of the Collatz function is an integer of arbitrary size. The behavior branches depending on the least significant bit of the input.

You can think of the least significant bit as the “head” of a machine similar to a Turing machine.

However, instead of moving the head along a tape, the Collatz function does one of two things:

1. Moves the symbols on the tape one space to the right (somewhat familiar territory for Turing Machines).
2. Rewrites all of the symbols on the tape to the left of the head, according to some algorithm. This algorithm makes the tape longer.

As we observed previously, the carry propagation implicit to addition makes the bits diffuse in a way that’s hard to generalize faster than simply performing the addition and seeing what results from it.

Proving that this Collatz machine halts for all positive inputs would also prove the Collatz Conjecture. But as we saw with proper Turing Machines, this might not be possible.

Pedants on the /r/math subreddit were quick to point out that this isn’t necessarily true, but the goal of this blog post was not to state a technically precise truth, but to explore the Collatz conjecture from a different angle.

The important disclaimer at the top isn’t some cop-out boilerplate I slap on everything I write to absolve me of any retribution for my mistakes. It’s actually important for everyone to read and understand it.

The entire point of this blog is “hey, here’s a neat idea to think about” not “here’s a universal truth about mathematics I discovered”. For that, I would have written an actual paper, not a furry blog. Unfortunately, I have no new insights to offer on anything, nor will I probably ever.

I recommend reading the comment I linked at the start of this quoted section, as it’s grounded in a more formal mathematics understanding than this blog post.

Is It Unsolvable?

With all this in mind, in the general case, the Collatz Conjecture may very well one day prove to be as undecidable as the Halting Problem.

Or, maybe someone will find a cycle within the integer space that fails to ever reach 1.

As it stands right now, there have been a lot of interesting approaches to try to solve it. The first Veritasium video linked above talked about some of these ideas.

Maybe we need new mathematic tools first. Or perhaps the Langlands project will uncover a relationship between unrelated areas of mathematical research that already exist today that will yield an answer to this nearly century-old conjecture.

Either way, I hope you find this topic… mildly interesting. Enough to appreciate the problem, not so much that you think you can solve it yourself.

Stay safe, don’t drink and derive, and happy hacking.

Header art: AJ and CMYKat.

#CollatzConjecture #define #HaltingProblem #mathematics #TuringMachines

Faffing about with complex numbers again

Integers have these things called complex conjugates. This is something I have just been learning about. Or not. You’ll soon see my mathematical shortcomings. This thing is, I think, a way to express them as complex numbers. (I think that was the takeaway of the videos I just watched).

I’d better quote the wiki because that feels like a rubbish explanation:

In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign.

Complex conjugate, Wikipedia

The first five look like this according to Google’s AI

I’m only actually interested in the first three because we could do something fun with those.

I previously showed my broken work as I wondered about the Collatz Conjecture over the complex plane. Mostly I wanted to know if complex numbers could be odd or even.

It’s possible to define even and odd Gaussian integers* in such a way that many of the familiar properties of the plain old integers are preserved, but it’s a little counterintuitive at first. The definition is that a+bi is even when a^2+b^2 is even (this is the norm of a+bi) and that a+bi is odd if it’s not even.

An answer from Mastodon that I shared here

So this got the old thinker ticking again. What if, I wondered, instead of 3x+1 or x/2, we used the complex numbers and went (3-i)x+1 and x/(2-0i) would that yield something interesting?

The Collatz Conjecture is that if you play a game where if a number is odd you times by three and add one and if even you divide by two that eventually you always get to one which loops to 4, 2, and back to 1. This is the only loop.

Test number 1 – powers of two

I asked Wolfram Alpha what 64/(2-0i) was. It is 32. Apply again and get 16. This seems to work all the way down.

Test number 2 – arbitrary odd numbers

I chose 7 – (3-i)7+1. The answer is 22-7i. That’s interesting.

Then I stopped and asked myself is 7 as a complex whatnot still odd? I asked what the complex conjugate of 7 is and, apparently, it is 7. So, I assume that’s the same as 7+0i but at this point, I clearly have no idea what I am talking about.

I’ve never let that stop me so let’s assume I am correct and have not utterly failed to understand some stuff.

7+0i is even if 7^2+0^2 is even. 49 is not even so, no 7 is not even on the complex doo-dah.

I’m not sure if this is good or bad but we have the Collatz step from 7 to 22 but with an extra -7i as baggage.

Test 3 – just run some numbers

I’m going to pick some smallish real integers and do this more complicated thing to them and see how long the real part stays correct for the simple version of Collatz.

Remember, I’m going (3-i)x+1 for complex odds and x/(2-0i) for evens.

7 -> 22-7i That’s odd for a complex number (the sum of the powers is 533)

22 should have gone to 11. Thus we have already deviated. Our new game leads us to 60-43i

And… I stopped.

First Conclusion

This game does not seem to play well over the complex plane. By “play well”, I mean do fun things.

Just out of idle curiosity, I asked what 22-7i over 2-0i was 11-3.5i. 11(3-i)+1 is 34-11i -> 17-5.5i…

Second conclusion

Well, I just got all excited over nothing. I truly hoped there was a nice pattern to find adding complex numbers to the Collatz thingy. Maybe there is but it might require writing some bad python to make a chart or something.

Ideas?

#CollatzConjecture #complexNumbers

There's a type of #maths problems thatt can be described as "deceptively simple". They sound straightforward when described, but solving them is another matter. #FermatsLastTheorem is one, the #CollatzConjecture is another.

I'm sure that the proof of the latter must have something to do with how the operation 3n+1 affects the binary representation of the number, but I'm not sure where to go next.

@KO6YQ
This would appear to imply a common origin of both the #CollatzConjecture and #TheTrolleyProblem . Someone should apply for a research grant to look into it.
#maths #logic #silliness #XKCD

#mathematics #CollatzConjecture #scripting I wanted to test my arithmetic routines, so I did some tests with big logs, and square roots, then I decided grandly to extend work on the Collatz conjecture :-)

wikidmedia says it's been checked to 2.95 x 10^20.

I can now announce (fanfare)...
2.950000000001 x 10^20 ;-)

___

p.s. (secretly, I'm just pleased it didn't fall through its execution stack like a stone through a wet paper bag)

Playing with Collatz

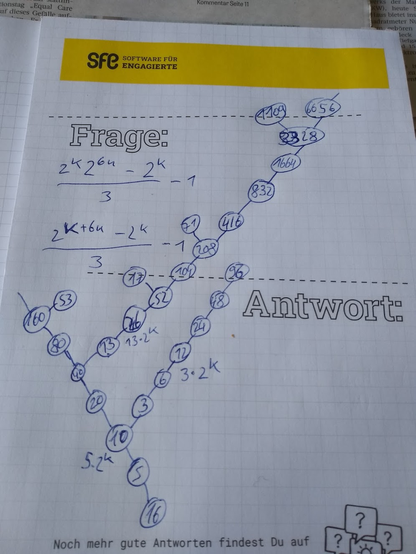
Previously, I had exhaustively proven that an exception to the Collatz Conjecture would have at least seven steps. I have expanded my exhaustive proof to show that an exception would have to have eight steps.

It’s not especially exciting but here are the tables of formulas and their solutions showing no loops under eight steps (by working out all possible patterns for up to seven steps).

#CollatzConjecture #maths

Can someone come and rescue me, please?

#math #CollatzConjecture

It's Three N Plus One as We Know It
#PuzzleASong
#HashTagGames
#maths #math
#CollatzConjecture

Oooh, exciting, Mirkowska and Salwicki (2023) claim to have proven the #CollatzConjecture, I totally missed this! Hans-Dieter Hiep (Leiden & CWI) is sceptical: https://www.hansdieterhiep.nl/is-collatz-conjecture-now-proven/

My poor #cpu.
I've spent the #morning on #coding and #implementing a #math problem that tries to find #candidates that break #collatzconjecture ... If you are thinking about this problem, go and touch grass and do something way more #productive with your time.

#mathproblem #stupidmathproblem #why

It's been _0_ days since I was nerdsniped by the #CollatzConjecture . :collatz_conjecture:

@lobsters hey @joshmillard , got some #CollatzConjecture info for you :collatz_conjecture:

Learning Rust Part 11 (Collatz Conjecture, Diffie Hellman, Series)

https://diode.zone/videos/watch/0b6c2ba4-d63c-44b7-856e-4e28a27460a3

[Matt Parker] on the completion of The Great Collatz Collab in which hundreds of schools picked 3 digit numbers to test the Collatz Conjecture, which were then collated into a single large map
https://youtu.be/lnpFqdQJAFA

The project resources including downloadable map:
https://think-maths.co.uk/collatz-collab

#youtube #CollatzConjecture #Collatz #maths #mathematics #STEM #mathstodon #mastomaths #math