Heute zu Gast um 16:15 im Sitzungszimmer des Mathematischen Instituts für die #MathematischeGesellschaft #Göttingen: Ko Sanders von der @unihannover über
"Distributions of positive type and applications in quantum field theory"
#UniGöttingen #GöttingenCampus #Mathematics #QuantumFieldTheory #Colloquium
This Thursday, I'm giving a #physics talk at PI about some recent results on #graph cohomology and topological #QuantumFieldTheory . For the title page, I took a photo of the local geese in Oxford. I wonder if the geese in Waterloo already have goslings now.
The slides will be on my website as always, if anyone is interested.
Today, I got to give one if my favorite lectures in quantum mechanics in my advanced undergraduate physics majors’ course.
The big concept is that the ultimate nature of reality is that particles are wave functions |Ψ> that exist outside of any coordinate system or physical space. The space that they occupy is instead a Hilbert Space. Their projection in what we percieve as our “space” is one representation of the fundamental nature of the particle — which is a field in a this abstract space. The properties of that field is what determines the properties and interactions of the particle.
This is where physics touches metaphysics — fun stuff!
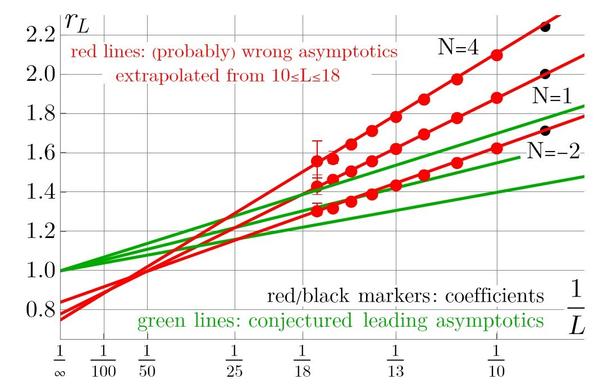
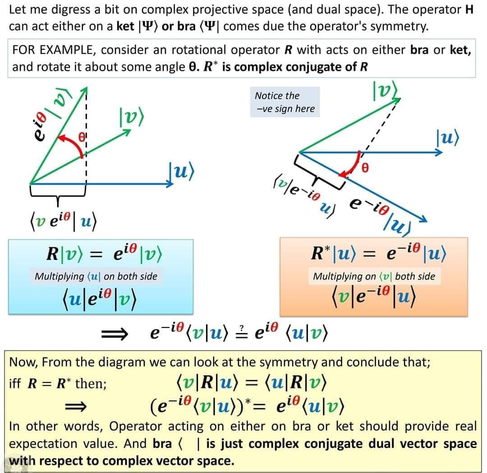
In a magazine article [1] on problems and progress in quantum field theory, Wood writes of Feynman path integrals, “No known mathematical procedure can meaningfully average an infinite number of objects covering an infinite expanse of space in general. The path integral is more of a physics philosophy than an exact mathematical recipe.”
This article [2] provides a method for averaging an arbitrary collection of objects; however, the average can be any number in the extension of the range of these objects. (Note, an arbitrary collection of these objects is a function.)
Question: Suppose anything meaningful has applications in quantum field theory. Is there a way to meaningfully choose a unique, finite average of a function whose graph matches the description in Wood's quote?
For more info, see this post [3].
[2]: https://arxiv.org/pdf/2004.09103
[3]: https://math.stackexchange.com/q/5052005/125918
#PathIntegral #quantum #FeynmanPathIntegral #mean #average #expectedvalue #quantumfieldtheory
New theoretical #physics preprint https://arxiv.org/abs/2412.08617
We looked at the asymptotic growth rate of the beta function in #quantumFieldTheory , and the relative importance of subdivergence-free #Feynmangraph s. These graphs correspond to integrals, and the size of the graph is measured by its loop number, which also indicates how hard it is to solve the integral. State of the art computations in realistic theories are anywhere between 1 and 6 loops. The asymptotics of the perturbation series is known from instanton calculations. We now showed (in a model theory), that the leading asymptotics describes the true growth rate only for more than 25 loops, way beyond anything that can realistically be computed.
This is good news: It tells us that asymptotic instanton calculations provide non-trivial additional information that can not be trivially inferred from low-order perturbation theory.
In the plot, the red dots are numerical data points for the subdivergence-free graphs in phi^4 theory up to 18 loops, the green lines are the leading instanton asymptotics.
📣 Tiburtius Prize 2024 for Gustav Uhre Jakobsen 🏆
Recognition award for visiting postdoc at AEI Potsdam
Gustav Uhre Jakobsen, a postdoc at the Humboldt University of Berlin and in the Astrophysical and Cosmological Relativity Department at the @mpi_grav in the Potsdam Science Park, will be awarded a “Tirburtius Prize – Prize of the Berlin Universities” for his dissertation.
The reviewer praises not only the impressive wealth of topics in Jakobsen's doctoral thesis titled “Gravitational Scattering of Compact Bodies from Worldline Quantum Field Theory” and the quality of the research results, but also the impact it has had in the research community.
➡️ https://www.aei.mpg.de/1202051/tiburtius-prize-2024-for-gustav-uhre-jakobsen
#ResearchAward #Berlin #PhDThesis #PhDLife #QuantumFieldTheory #GeneralRelativity
🚨 New #preprint !
We study a stochastic PDE whose solutions want to be close to constant -1 or +1. But because it’s stochastic, the solutions occasionally jump between those two optima. How often, on average?
In technical terms, we study a certain nonlinear wave equation whose invariant measure is the \( \phi^4 \) #QuantumFieldTheory. The average transition time is called an Eyring–Kramers law, asymptotic in the low-temperature limit. It has already been derived for 2D stochastic heat equation and 1D wave; we extend it to 2D and 3D wave equations.
Joint work with my PhD advisor Nikolay Barashkov. #MathematicalPhysics #MathPhys
#quantumphysics #quantumfieldtheory
Quantum physics lecture video link
https://youtu.be/cbF-3tt-c_0
Two years ago, I began writing my #doctoralThesis in theoretical #physics. Most effort went into giving a very detailed pedagogical account of what the #renormalization #HopfAlgebra in #QuantumFieldTheory does, and why it is natural and transparent from a physical perspective.
One year ago, my referees recommended in their reports to publish the thesis as a book, and today I received the printed copies!
It was exciting to go through all the steps of actually publishing a book, and I hope that it will be of use to convince physicists that the Hopf algebra structure in #QFT is not a weird mathematical conundrum, but it actually encodes the very way physicists have been thinking of renormalization since the 1950s: Parametrize a theory by quantities one can actually measure, instead of fictional expansion parameters.
https://link.springer.com/book/10.1007/978-3-031-54446-0
#Mathematician Jim Simons died
on🪦2024 May.10👇
http://bit.ly/3QIEmRc
In 1962 he made contributions to #StringTheory based on topological invariants in #QuantumFieldTheory
In 1964 he joined🇺🇸 🕵️#NSA to work as #CodeBreaker
Then moved to markets to create a #HedgeFund with which he got a net worth of💰uS$ 31.4 billion.
In #QuantumFieldTheory, scattering amplitudes can be computed as sums of (very many) #FeynmanIntegral s. They contribute differently much, with most integrals contributing near the average (scaled to 1.0 in the plots), but a "long tail" of integrals that are larger by a significant factor.
We looked at patterns in these distributions, and one particularly striking one is that if instead of the Feynman integral P itself, you consider 1 divided by root of P, the distribution is almost Gaussian! To my knowledge, this is the first time anything like this has been observed. We only looked at one quantum field theory, the "phi^4 theory in 4 dimensions". It would be interesting to see if this is coincidence for this particular theory and class of Feynman integrals, or if it persists universally.
More background and relevant papers at https://paulbalduf.com/research/statistics-periods/
#quantum #physics #statistics
C
Reframing the holographic principle in the context of nested gravastars could explore how these structures manage information and geometry without singularities, potentially offering a new perspective on how the universe's informational content is organized and represented.
#quantumfieldtheory #generalrelativity #gravastars #astrophysics #theoreticalphysics #quantummechanics #informationtheory
#DeanRickles - Is #Time #Fundamental?
https://www.youtube.com/watch?v=1TkPn-QNYtk
#Philosophy #PhilosophyOfTime #Logic #Metaphysics #PhilosophyOfScience #Science #Emergence #Physics #Entropy #StatisticalMechanics #GR #GeneralRelativity #SpecialRelativity #Newton #Einstein #QM #QuantumMechanics #QuantumTheory #FieldTheory #Space #SpaceTime #QuantumFieldTheory #CloserToTruth #RobertKuhn
I am currently investigating an analogy between geodesic deviation from GR and the electromagnetic (Lorentz + Coulomb) force in QED. Once I got all the mathematical details worked out, I will make a thread about this, but I am tripping over the details of how to solve the classical Dirac equation perturbatively in a constant external EM field (mainly distribution-theoretical Fourier stuff). Does anyone here have a good reference on this?
#physics #theoreticalphysics #quantumfieldtheory #quantummechanics
#Dilbert #SimulatedReality #QuantumPhysics #HolographicUniverse #cosmology #physics #ArtificialReality #QuantumFieldTheory #FreeWill #epistemology
Scott Adams 🤬
https://en.wikipedia.org/wiki/Scott_Adams#Race
[2023-02-27] Distributor, newspapers drop 'Dilbert' comic strip after creator's racist rant
https://www.npr.org/2023/02/26/1159580425/newspapers-have-dropped-the-dilbert-comic-strip-after-a-racist-rant-by-its-creat
Video (Adams): racist troll, extraordinaire. 😡
https://www.youtube.com/watch?v=K6TnAn7qV1s
#SystemicRacism #CriticalRaceTheory #discrimination #whiteSupremacism #BLM #BlackLivesMatter #BlackTransLivesMatter
.
#FrankWilczek - How is the #Cosmos Constructed?
https://www.youtube.com/watch?v=58uLU_wbsM8&ab_channel=CloserToTruth
#Philosophy #PhilosophyOfScience #Science #PhilosophyOfCosmology #Cosmology #Physics #Astrophysics #Particles #Fields #SubatomicParticles #ParticlePhysics #QM #QuantumMechanics #QuantumPhysics #QuantumFields #QuantumFieldTheory #Maxwell #Electromagnetism #CloserToTruth #RobertKuhn
Why does anything exist? Well…
What if black holes are observers in the quantum sense? What if the #universe itself is an observer in the quantum sense? That is the question.
So anyway #QuantumFieldTheory in curved spacetime is pretty dope. I love how mind-bending #QuantumPhysics is and how this video plays into my interest in #cosmology and #philosophy.
I’ll just pass this along. Anton Petrov did a great video on the topic.
Another publications of the thematic programme on #QuantumFieldTheory at the Frontiers of the #StrongInteraction 😍
Wen Chen, Ming-xing Luo, Tong-Zhi Yang, Hua Xing Zhu / Soft Theorem to Three Loops in QCD and N=4 Super Yang-Mills Theory
This is also a result of the thematic programme on #QuantumFieldTheory at the Frontiers of the #StrongInteraction ⬇️
🟩 Andrea Ghira, Simone Marzani, Giovanni Ridolfi / A consistent resummation of mass and soft logarithms in processes with heavy flavours 🟩
