Faithful logic embeddings in HOL (Deep and shallow). ~ Christoph Benzmüller. https://arxiv.org/abs/2502.19311 #ITP #TheoremProving #IsabelleHOL #Logic #Math
#TheoremProving
REAL-Prover: Retrieval augmented Lean prover for mathematical reasoning. ~ Ziju Shen et als. https://arxiv.org/abs/2505.20613 #AI #TheoremProving #LeanProver #Math
The Department of Computer Science, University of Oxford has released recordings of the recent Strachey Series Lectures featuring Leo de Moura and Kevin Buzzard:
1️⃣ "Formalizing the Future: Lean's Impact on Mathematics, Programming, and AI" - Leo de Moura, Chief Architect of Lean
Leo discusses how Lean provides a framework for machine-checkable mathematical proofs and code verification, enabling collaboration between mathematicians, software developers, and AI systems. He also outlines the work the Lean Focused Research Organization does to expand Lean’s capabilities and support the community.
➡️ Watch Leo's lecture here: https://podcasts.ox.ac.uk/formalizing-future-leans-impact-mathematics-programming-and-ai
2️⃣ "Will Computers Prove Theorems?" with Kevin Buzzard, Professor of Mathematics, Imperial College
Kevin examines the potential for AI systems and theorem provers to assist in mathematical discovery, addressing whether computers might someday find patterns in mathematics that humans have missed, and discusses the integration of language models with formal verification systems.
➡️ Watch Kevin's lecture here: https://podcasts.ox.ac.uk/will-computers-prove-theorems
#LeanLang #LeanProver #FormalVerification #Mathematics #AI #TheoremProving #OxfordCS
Introducing #DeepSeekProverV2 - a new #opensource #LLM designed for formal theorem proving in Lean 4.
The model builds on a recursive #TheoremProving pipeline powered by the company's DeepSeek-V3 foundation model.
Learn more: https://bit.ly/3ZlTt7h
The Lean FRO team met synchronously in Amsterdam last week for our annual team retreat, and to discuss upcoming work and our Year 3 roadmap! 🇳🇱✨
We had very productive discussions around Lean's future in mathematics, software and hardware verification, and AI for math. It was energizing to see our team's commitment to Lean's continued growth in each of these domains.
We're cooking up many exciting developments that will support both our mathematical community and our growing base of software verification users. Stay tuned for our full Y3 roadmap publication at the end of July!
#LeanLang #LeanProver #Lean4 #FormalVerification #Programming #Mathematics #TheoremProving
📊 Latest in Math Research:
- Near-linear time graph coloring algorithm
- Terrence Tao's flexible proof assistant
- Seminar on Hyper-Catalan series (May 13)
#Mathematics #TheoremProving
Channeling some PhD vacancies from our 🇳🇱 friends:
Six fully-funded PhD positions (4 years) in the project "Cyclic Structures in Programs and Proofs – New Harmonies in Software Correctness by Construction"
Deadline: Friday, May 23, 2025
🤖 DeepSeek silently dropped a 671B math-proof machine — no hype, just results.
🧠 88.9% MiniF2F
💣 Built for Lean 4
🔥 Outperforms past models, benchmarks Putnam problems
👀 Nobody’s talking about it… yet.
#AI #LLM #DeepSeek #MathGPT #AGI #TheoremProving #OpenSource #DeepSeekProverV2
Prover-V2 is insane. Full breakdown:
https://deepseekagi.org/deepseek-prover-v2-ai-breakthrough-in-math-theorem-proving/
DeepSeek Releases Massive 671B Prover V2 Model For Mathematical Theorem Proving Ahead of R2 Release
#AI #ChinaAI #DeepSeek #OpenSourceAI #Math #TheoremProving #Lean4 #MachineLearning #DeepLearning #MathAI
Call for Papers
16th International Conference on Interactive Theorem Proving — ITP'25
Reykjavik, Iceland
27 September – 3 October 2025
https://icetcs.github.io/frocos-itp-tableaux25/itp/
ITP is concerned with all aspects of interactive theorem proving, ranging from theoretical foundations to implementation aspects and applications in program verification, security, and the formalization of mathematics.
- Abstract submission deadline: 12 March 2025
- Paper submission deadline: 19 March 2025
- Author notification: 23 May 2025
- Camera-ready copy due: 27 June 2025
#formalization #theoremproving #proofassistants #verification #CfP
@wren_h Hi !!
It's great to have you here, and pleased that you're not some sort of robot. Not sure where you got the message that you should make such a post, but it's definitely a good idea to start interacting. There are no algorithms here to fill your timeline(s) with posts that other things think you should be interested in.
It's worth putting hashtags on posts to make them findable. Things like:
#DependentTypes or #TypeTheory or #TheoremProving or #DesignOfProgrammingLanguages or similar. Then when you've done that, have a look at your own post and click on the hashtags to see who else is talking about them.
Good luck!
The pre-print for the #ICPC paper “Pinpointing the Learning Obstacles of an Interactive Theorem Prover” by @sarantja @azaidman and yt is now available at https://sarajuhosova.com/assets/files/2025-icpc.pdf
I very much hope this will inspire more research on the usability and accessibility of the languages we build going forward!
Abstract:
Interactive theorem provers (ITPs) are programming languages which allow users to reason about and verify their programs. Although they promise strong correctness guarantees and expressive type annotations which can act as code summaries, they tend to have a steep learning curve and poor usability. Unfortunately, there is only a vague understanding of the underlying causes for these problems within the research community. To pinpoint the exact usability bottlenecks of ITPs, we conducted an online survey among 41 computer science bachelor students, asking them to reflect on the experience of learning to use the Agda ITP and to list the obstacles they faced during the process. Qualitative analysis of the responses revealed confusion among the participants about the role of ITPs within software development processes as well as design choices and tool deficiencies which do not provide an adequate level of support to ITP users. To make ITPs more accessible to new users, we recommend that ITP designers look beyond the language itself and also consider its wider contexts of tooling, developer environments, and larger software development processes.
#Agda #TheoremProving #DependentTypes #Usability #Accessibility #ICPC25
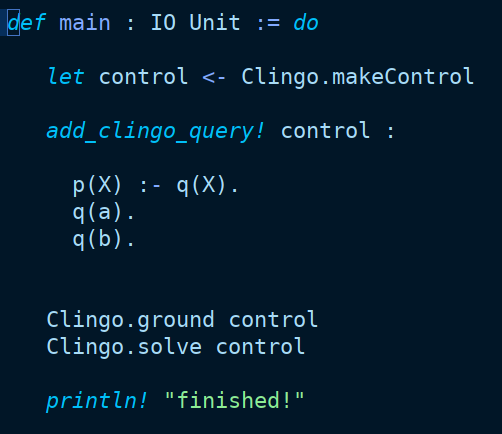
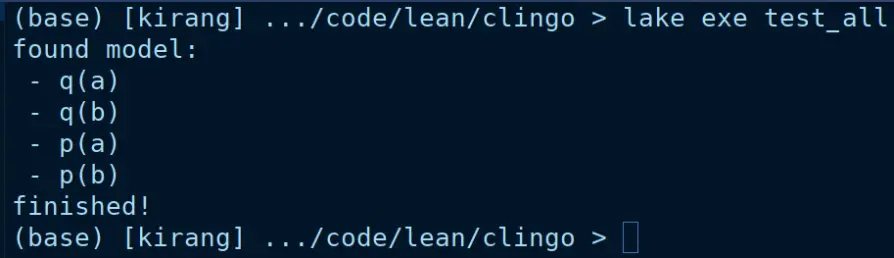
I stayedd at the lab wayyyyy late to finish this off, but I'm pretty proud of this!!! I've been playing with macros in Lean4 #Lean4 recently, and they make me really exciteddd!!!
I've implemented a DSL in lean that uses the grammar of the constraint logic programming language Clingo, and solves queries through the FFI.
Honestly really blown away by the macro support in Lean. The way they combine extensible syntax and type system support is just mindblowing, it's honestly the best macro system I've ever used so far, and I can't even believe that I'm writing all this in a dependently typed language to boot.
You can check it out here: https://github.com/kiranandcode/cleango
@leanprover@functional.cafe
#ProgrammingLanguages #Macros #Lean4 #TheoremProving
I'm trying to use Z3 to solve a logic puzzle, mostly as a chance to learn more about Z3. I'm stuck on a couple of things out of the gate:
How do people usually interact with Z3 in practice? Manually writing smtlib doesn't seem like it would scale. Do people use the Z3 bindings to Python, Java, etc. or are people using libraries to generate smtlib syntax which then gets fed in?
I'm looking at the TypeScript bindings. There's a "high level" set of bindings which seems incomplete (no support for datatype declarations, for example) and a "low level" set of bindings that seems more featureful. I get the vibe that the high level bindings aren't getting a lot of usage or maintenance. Can anyone confirm or give background here? Is TS simply the wrong language to use, or am I still likely to be writing Z3 in a modern-ish way by using the low level bindings?
proving some theorems
Exciting new blog post alert! 🌟 Dive into the world of automated theorem proving with AlphaProof, revolutionizing mathematical proofs. 🧠✨
https://www.eliza-ng.me/post/alphaproofmathe/
#Mathematics #AlphaProof #TheoremProving
📢 Excited to announce I'll be giving a lecture on "Interactive Theorem Proving in Isabelle/HOL & Its AI-Driven Automation Efforts" at the EuroProofNet Summer School on AI for Reasoning & Processing of Mathematics! 🧠🖥️
Join us at Kutaisi International University, Georgia, from June 24th-28th, 2024. Learn more & register here: https://europroofnet.github.io/Kutaisi24/
[New Blog Post] Termination Checkers: Playing with AProVE https://www.philipzucker.com/termination_checker/ #logic #theoremproving #verification
*sigh* Apparently every other year when I pick up Coq to do some light theorem proving I need to learn again the hard lesson that you never do `intros.`, but only `intros <exactly this> <exactly that>.`
Listening to the Type Theory Forall podcast with Kevin Buzzard (@xenaproject). Really interesting view on how theorem provers are viewed in mathematics and where formal mathematics is heading. It's making me think about what the Agda community could learn from this. Strongly recommended you give it a listen!
https://www.typetheoryforall.com/2023/01/16/26-Kevin-Buzzard.html#07a08a85