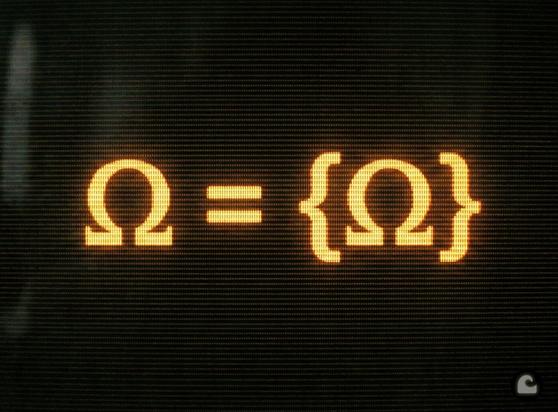So we have { 1, 2 } ∈ Fin₁ ⊆ Fin₁ₐ ⊆ Fin₂ ⊆ Fin₃ ⊆ Fin₄ ⊆ Fin₅ ⊆ Fin₆ ⊆ Fin₇

If a set is in Fin₁ then it is considered finite by all the other definitions.

But since the axiom of choice is equivalent to saying every set can be well-ordered, if we accept it VII-finite sets are equinumerous with a finite ordinal and so Fin₇ ⊆ Fin₁ and so the differences between these definitions collapse and ZF becomes ZFC, which is a widely accepted basis for Set Theory.

My consultation with math resources was inspired by a blog post:

https://www.infinitelymore.xyz/p/what-is-the-infinite

#Metamath #ZFC #SetTheory #AxiomOfChoice #FiniteSet #Infinity

Proposition: Russell's paradox is a grammatical artifact of set-theoretic language, not a fundamental limitation on self-reference.

Evidence:

Category theory permits self-morphisms (id_X : X → X) without paradox
Aczel's AFA permits self-containing sets by reinterpreting membership as graph structure
Process algebras (π-calculus) permit self-invoking processes without paradox

The key distinction:

"The barber who shaves all and only those who don't shave themselves" → Paradox
"The process that processes itself" → No paradox. That's just recursion.

The paradox isn't from self-reference. It's from the exclusion clause — "only those who don't." That's container logic: you're either IN or OUT.

Process logic has no exclusion clause. A function can call itself. A mirror can reflect a mirror. A wave can contain wave.

Conclusion: Self-reference is only paradoxical when forced through container grammar (discrete membership, exclusion). In process grammar (continuous relationship, inclusion), it just runs.

Pointers to related work welcome.

{🌊:🌊∈🌊}

#RussellsParadox #SetTheory #CategoryTheory #Logic #Mathematics #Philosophy #SelfReference

Thinking about non-well-founded set theory (Aczel 1988) and the Quine atom Ω = {Ω}.

Russell's paradox arises from self-reference in sets. But Aczel showed self-containing sets are consistent if you drop the Foundation Axiom.

Here's what I'm chewing on: Russell's paradox feels like a linguistic trap as much as a logical one. Sets are framed as containers (nouns). A container containing itself → paradox.

But Ω = {Ω} works because we're describing relationship, not containment. The set doesn't "hold" itself like a box — it refers to itself like a pattern.

Has anyone explored whether the noun/verb distinction (container vs. relationship) is doing hidden work in self-reference paradoxes?

Pointers to literature welcome.

#SetTheory #MathematicalLogic #SelfReference #FoundationsOfMathematics

A New Bridge Links the Strange Math of Infinity to Computer Science

https://fed.brid.gy/r/https://www.wired.com/story/a-new-bridge-links-the-strange-math-of-infinity-to-computer-science/

Happy birthday of set theory, for all those who celebrate!

On December 7, 1873, Georg Cantor (https://en.wikipedia.org/wiki/Georg_Cantor) wrote a letter (https://www.aleph1.info/?call=Puc&permalink=cd1_Briefe_Z4) to Richard Dedekind in which he showed that there are more real numbers than integers and that therefore different kinds of infinity exist. Cantor's proof at this time is not the “diagonalisation” proof that is now usually given.

December 7, 1873 is also the 50th birthday of Leopold Kronecker (https://en.wikipedia.org/wiki/Leopold_Kronecker), which is ironic, given the heavy conflicts they would have about set theory.

The birthday of set theory is usually celebrated with a birthday cake that has ℵ₀ candles on it, but you can take fewer if you don't have the space for them. 🕯️

#SetTheory #Mathematics #HistoryOfMathematics #HistoryOfScience #GeorgCantor #LeopoldKronecker

Any #mathematics professors want to take a shot at explaining to someone with say a typical math major undergrad background what the deal is with the recent introduction of exacting and ultraexacting cardinals?

#math #maths #settheory #zfc

https://arxiv.org/abs/2411.11568

Readings shared November 24, 2025. https://jaalonso.github.io/vestigium/posts/2025/11/25-readings_shared_11-24-25 #CompSci #CoqProver #ITP #LeanProver #Logic #Math #Physics #SetTheory #TypeTheory

Set theory with types. ~ Lawrence Paulson. https://lawrencecpaulson.github.io//2025/11/21/Typed_Set_Theory.html #Logic #Math #CompSci #SetTheory #TypeTheory

"Like parsley in Greek food: Elementary set theory and the case for DM1" by Siddharth Bhaskar (https://dblp.org/pid/170/0077.html) got accepted at SIGCSE TS 2026.

https://sigcse2026.sigcse.org/details/sigcse-ts-2026-Papers/164/Like-parsley-in-Greek-food-Elementary-set-theory-and-the-case-for-DM1

#SIGCSE #setTheory #CSEducation #math #discreteMath #computerScience

Readings shared October 23, 2025. https://jaalonso.github.io/vestigium/posts/2025/10/24-readings_shared_10-23-25 #AI #Agda #ITP #LLM #LeanProver #Math #SetTheory

And here's a "general audience" (or "popular math") description of the general theme in this paper, and much of my work in general. Don't hesitate to ask for more details!

In this paper I explore the boundaries of what is mathematically possible when constructing universes of set theory. A "universe of set theory" can be thought of as a model for all of mathematics, and what we, set theorists, like to do, is build different kinds of such universes.
We have two main tools:
1. Take a universe, and add stuff, to create a larger one;
2. Take a universe, and define inside of it a smaller one.
In my paper I use both methods: I extend a given universe and build a larger one, in which I use a specific definition to construct a smaller universe.
The cool thing is, that I can use that definition again - to get an even smaller universe. And again, and again - infinitely many times!

#math #SetTheory #multiverse #PopularMath #PopularScience

My paper has now been officially published!

https://www.worldscientific.com/doi/10.1142/S0219061325500229

#math #paper #publication #Logic #SetTheory

Constructive ordinal exponentiation. ~ Tom de Jong, Nicolai Kraus, Fredrik Nordvall Forsberg, Chuangjie Xu. https://arxiv.org/abs/2501.14542 #ITP #Agda #SetTheory

Readings shared October 14, 2025. https://jaalonso.github.io/vestigium/posts/2025/10/15-readings_shared_10-14-25 #FunctionalProgramming #Haskell #ITP #IsabelleHOL #LeanProver #Logic #Math #Python #RustLang #SetTheory

ZF style set theory in Knuckledragger I. ~ Philip Zucker. https://www.philipzucker.com/zf_knuckle1/ #Python #Logic #SetTheory

A gentle introduction to the axiom of choice. ~ Andreas Blass, Dhruv Kulshreshtha. https://arxiv.org/abs/2509.01830 #Math #SetTheory

Set theory as a unified framework

" #settheory, the ranges of binders are the sets. Thus, beyond its simplifying advantage of removing types, set theory will get more power by its strengthening axioms which amount to accept more classes as sets."
https://settheory.net/foundations/unif#:~:text=set%20theory%2C%20the%20ranges%20of%20binders%20are%20the%20sets.%20Thus%2C%20beyond%20its%20simplifying%20advantage%20of%20removing%20types%2C%20set%20theory%20will%20get%20more%20power%20by%20its%20strengthening%20axioms%20which%20amount%20to%20accept%20more%20classes%20as%20sets.

@LeoTsai14 While they do not actually call it so, set theoreticians do a lot of work in a category in which the objects are the models of set theory and the arrows are the elementary embeddings (https://en.wikipedia.org/wiki/Elementary_equivalence#Elementary_embeddings) between them.
Models of (ZFC-like) set theories have the interesting property that the maps between them are to some amount determined by the mappings between their classes of ordinals: If this map is an isomorphism, the whole map is one (https://en.wikipedia.org/wiki/Critical_point_(set_theory)).
You may also have a look at inner model theory (https://en.wikipedia.org/wiki/Inner_model_theory), I think.

#SetTheory #ModelTheory #MathematicalLogic #Categories

What is the difference between intensional and extensional logic? - Philosophy Stack Exchange
"The predicates "having a kidney" and "having a heart" clearly have different senses, but as a matter of contingent fact everything that has a kidney has a heart: hence we case the two terms are co-referential. The set of the renates = the set of the cordates, because set membership is extensional. First order logics, including set theory are all extensional in this sense. It doesn't matter whether we are talking about the set of the renates or the set of the cordates, because they are the same set, and we know they're the same set, because we define a set extensionally--i.e. purely by the reference of the terms. We don't need to know what the terms "renate" and "cordate" really mean, we just need to know which things they refer to."
#settheory
/frege https://philosophy.stackexchange.com/questions/16164/what-is-the-difference-between-intensional-and-extensional-logic#:~:text=The%20predicates%20%22having,they%20refer%20to.