🧠 TODAY at #CCN2025 ! Poster A145, 1:30-4:30pm at de Brug & E‑Hall. We've developed a bio-inspired "What-Where" CNN that mimics primate visual pathways - achieving better classification with less computation. Come chat! 🎯
Presented by main author Jean-Nicolas JÉRÉMIE and in cosupervision with Emmanuel Daucé
https://laurentperrinet.github.io/publication/jeremie-25-ccn/
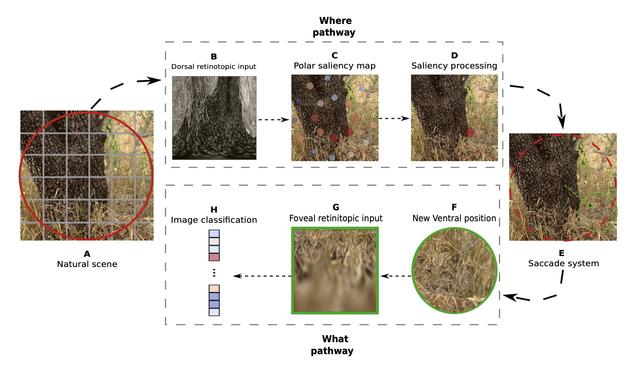
Our research introduces a novel "What-Where" approach to CNN categorization, inspired by the dual pathways of the primate visual system:
The ventral "What" pathway for object recognition
The dorsal "Where" pathway for spatial localization
Key innovations:
✅ Bio-inspired selective attention mechanism
✅ Improved classification performance with reduced computational cost
✅ Smart visual sensor that samples only relevant image regions
✅ Likelihood mapping for targeted processing
The results?
Better accuracy while using fewer resources - proving that nature's designs can still teach us valuable lessons about efficient AI.
Come find us this afternoon for great discussions!
#CCN2025 #ComputationalNeuroscience #AI #MachineLearning #BioinspiredAI #ComputerVision #Research