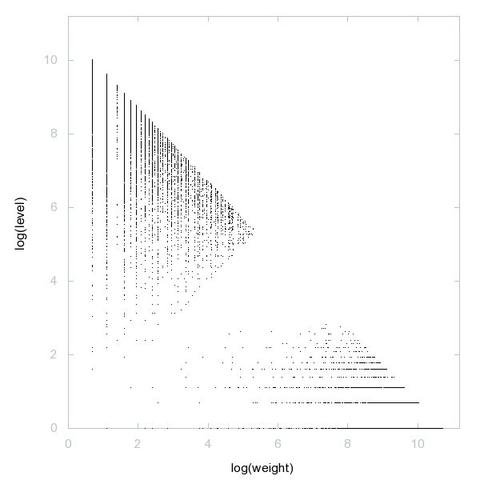
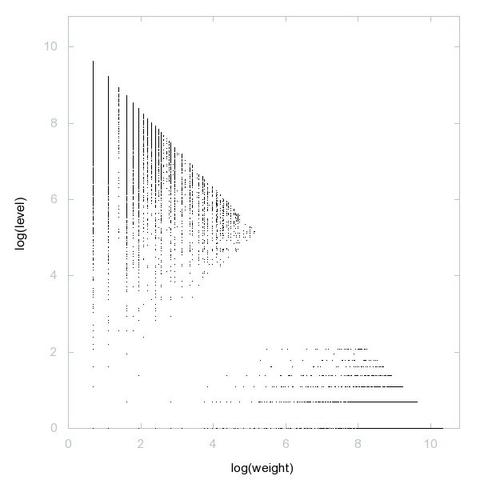
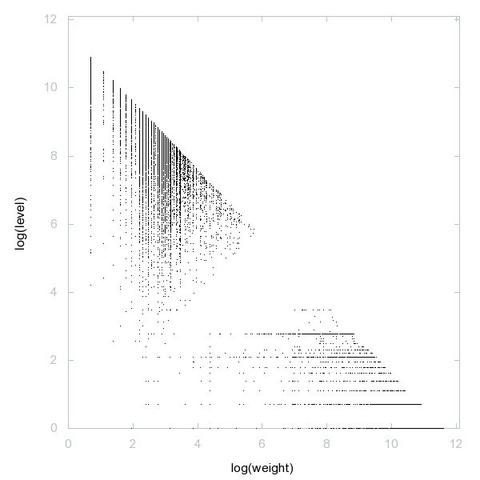
One day, one decomposition
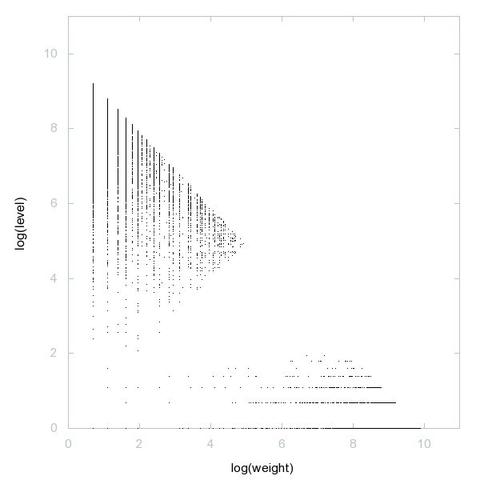
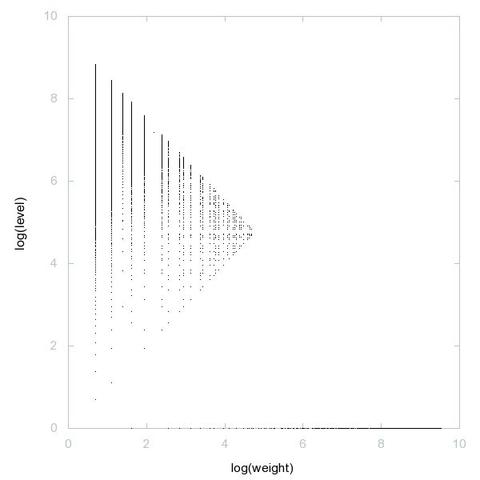
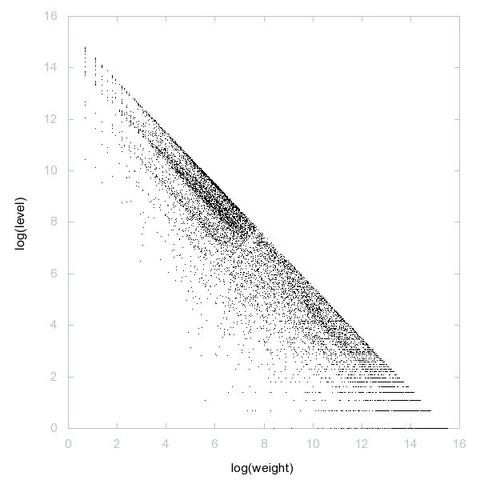
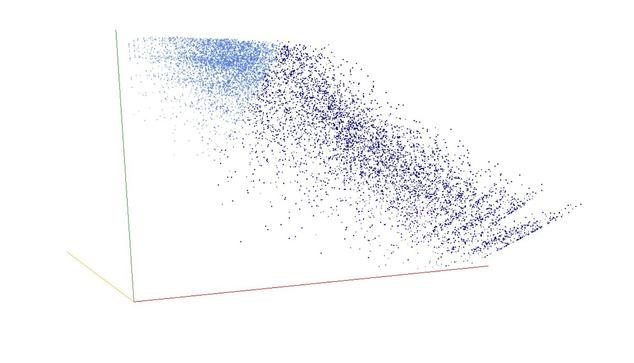
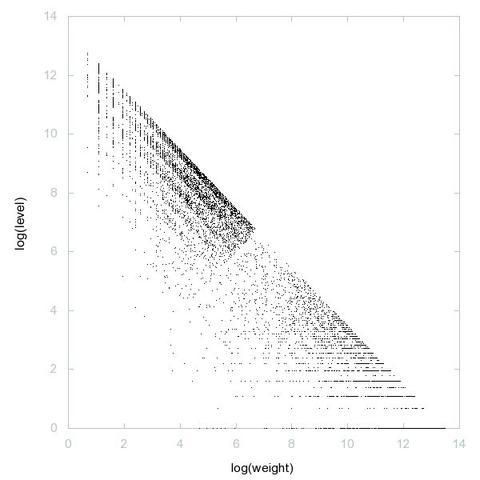
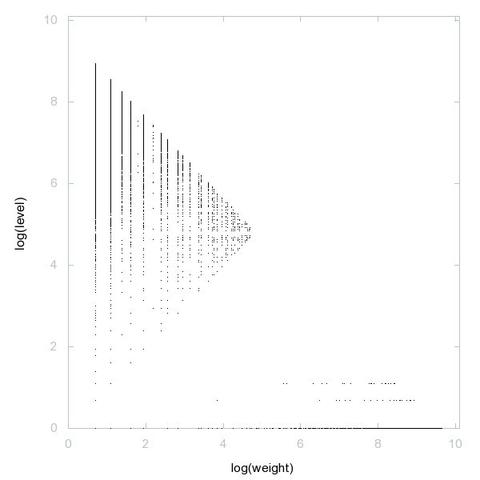
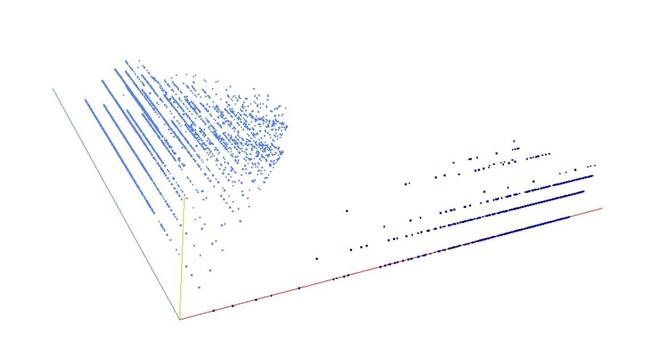
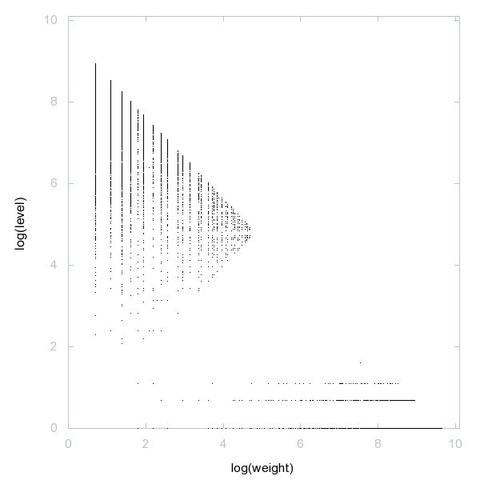
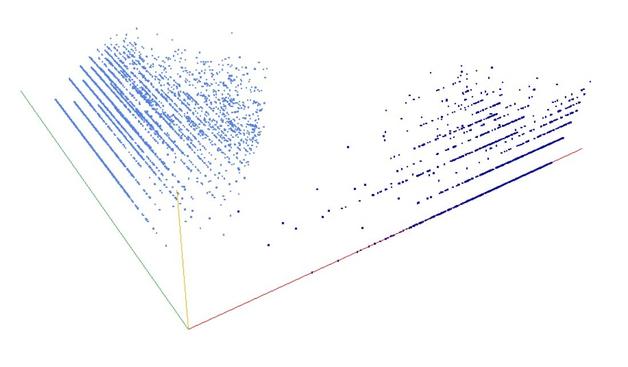
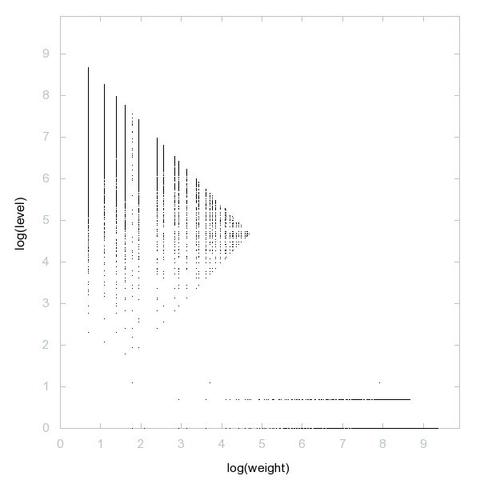
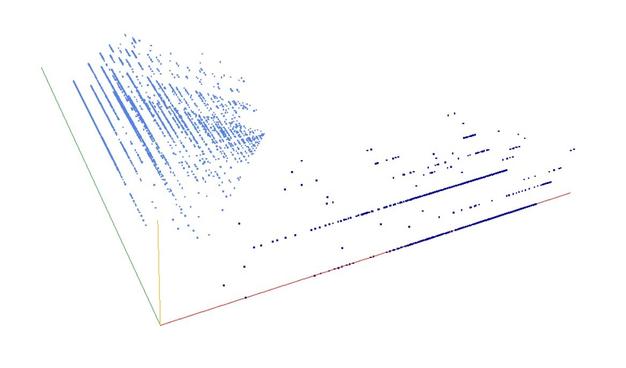
A000028: Let k = p_1^e_1 p_2^e_2 p_3^e_3 ... be the prime factorization of n. Sequence gives k such that the sum of the numbers of 1's in the binary expansions of e_1, e_2, e_3, ... is odd.
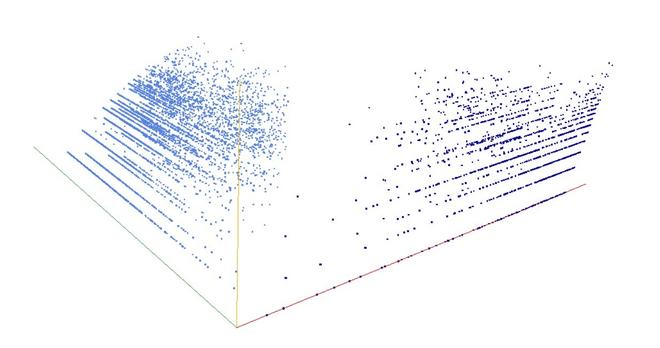
3D graph, threejs - webGL ➡️ https://decompwlj.com/3Dgraph/A000028.html
3D graph Gen, threejs animation ➡️ https://decompwlj.com/3DgraphGen/A000028.html
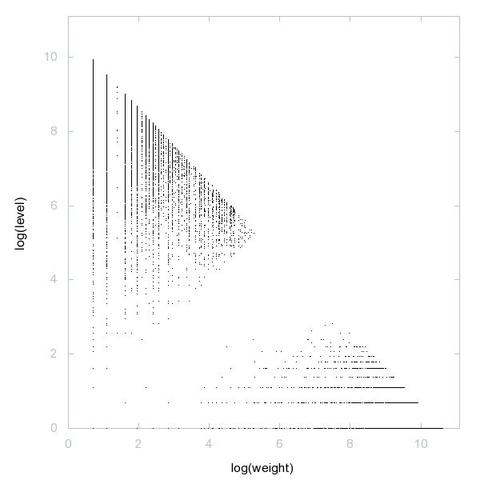
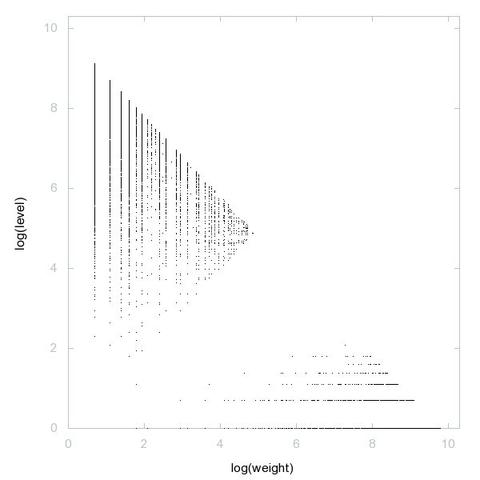
2D graph, first 500 terms ➡️ https://decompwlj.com/2Dgraph500terms/A000028.html
#decompwlj #math #mathematics #sequence #OEIS #javascript #php #3D #numbers #primes #factorization #PrimeNumbers #binary #expansions #graph #threejs #webGL