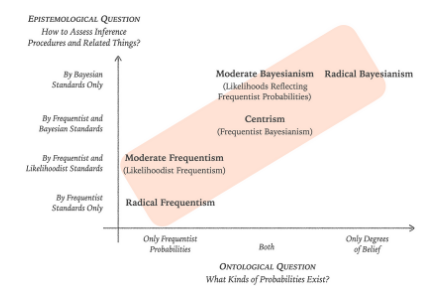
Where are you ? #probabilitytheory #philosophy

An Introduction to Stochastic Calculus

https://bjlkeng.io/posts/an-introduction-to-stochastic-calculus/

#HackerNews #StochasticCalculus #Introduction #MathFinance #ProbabilityTheory #Education

2025 is looking like a great year for work at the intersection of #categorytheory, #systemstheory, #controltheory, #machinelearning and #probabilitytheory, this thread will be a very biased collection of works (in no specific order) I'm hoping to read as soon as possible!

Starting with:
"Logical Aspects of Virtual Double Categories"
https://mastoxiv.page/@arXiv_mathCT_bot/113921693949589956

I don't always share #videos of a #dragqueen giving a #tierlist regarding the #films and #games found on #OsamaBinLaden laptop, but when I do, it's Sunday December 29th 2024... I'm not expecting this to happen again. The #ProbabilityTheory be damned.

This #toot brought to you by the #WokeDetector. Say "up yours, you #woke #moralists" to games that try to groom your kids with the trans liberal agenda.

I Ranked Every Movie AND Show On Osama Bin Laden's Hard Drive
https://youtube.com/watch?v=FIM_aG8ZsVA

Given that I am surrounded by Mathematicians here, let me ask for help for what should be a simple problem I can't seem to be able to solve:
Assume you have n fair dice with m faces (i.e. each can roll an integer from 1 to m with a uniform probability). You roll all n, and keep the k (with 0<k<=n) highest results. What is the probability that the sum of the k dice you kept is X?
(If one keeps all the dice, probability-generating functions give the answer straightforwardly. If I roll 2 dice and keep 1 I can easily enumerate the outcomes and calculate the probabilities, but I am stumped by the general case).

#ProbabilityTheory #IShouldKnowHowToSolveThisButIDoNot 😞

Fun little exercise: prove that if two Bernoulli random variables are perfectly correlated then they must be equal. #probabilitytheory

#FinishedReading #Boole 's Laws of Thought, whose final chapters partly shift attention from #logic to #probabilityTheory and #philosophyOfScience . I don't have a strong sense of his historical standing in either discipline, although for probability there is https://en.m.wikipedia.org/wiki/Boole%27s_inequality . The attraction of probability is clear, with its range of values from 0 to 1, use of '1 -' for negation, multiplication for conjunction (of independent events) etc. There are rhymes here with his logic at least

Several months ago, I came up with a #probability problem when thinking about physics-sim games. I took 1 or 2 statistics courses in college, but I'm at a complete loss for where to start. Anyone good at #statistics want to take a look?

Consider n sinusoids of the form A_i sin(fx+theta_i). The sum of all of these sinusoids is of the form Asin(fx+theta). Supposing that each theta_i is uniformly distributed (uniformly distributed over any half-open interval of length 2pi, the specific interval doesn't change the situation), and given each A_i, what is the expected value of A, and what else can be said about its distribution?

I don't remember exactly where I got, but I do remember being able to use some trig identity to express the sum in terms of cos(theta_i-theta_j)-like terms, and these terms are *not* statistically independent.

#probabilitytheory

There are many situations in the real world where small initial differences can easily grow into very large differences just out of pure chance.
Since we are on a social network, let's create a toy model* where a number of posts all have the same probability to be reposted/shared/boosted by any person seeing them. Since the more people see a post, the more people have a chance of boosting it, the posts with more visibility are also the ones that are likely to gain more visibility. So small initial fluctuations (just one or two extra boosts at the beginning) can lead a post to skyrocket in popularity, even though it is not intrinsically "better" than any of the other.
If we simulate this process numerically and make a histogram of the result, we see that the distribution of how many boosts a post had rapidly grows a tail, with most posts having no visibility whatsoever, and a few having a LOT more than the average.
#ITeachPhysics #ProbabilityTheory #ToyModel

* In the #Physics jargon, a "toy model" is a very simple (often unrealistic) model, which nevertheless capture the essence of the problem, without being burdened by all the real world complications. If you ever heard about spherical cows in vacuum, that is a toy model!

While waiting for a meeting to start, I decided to revisit one of the classics
#graphicalmodels #probabilityandstatistics #probabilitytheory #probability #DAG

James Bernoulli on #ProbabilityTheory and the application of #statistics

"I cannot conceal the fact here that in the specific application of these rules, I foresee many things happening which can cause one to be badly mistaken if he does not proceed cautiously." -1713, pt 4, cpt III

Now (7pm ET Wed) watch https://youtu.be/QS0VmCD9YLU(FEEL FREE TO SUBSCRIBE TO YOUTUBE
@hajiaghayi
FOR FUTURE LESSONS) Lesson 14: Introduction to Algorithms by Mohammad Hajiaghayi: We talk about #Probability (Part 2) useful for designing #randomized #algorithms

#algorithms, #design, #induction, #recursive, #randomizedalgorithms, #probability, #randominput ,
#probabilitytheory, #randomvariables, #expectations, #variance, #Bernoulli, #Binomial, #Poisson, #Normaldistribution, #Gaussian, #Python, #numpy.random, #scipy.stats, #correlation, #Pearson, #spearman, #geeksforgeeks , #hackerrank, #leetcode, #cs, #computerscience

In 1654, letters between Blaise Pascal and Pierre de Fermat established the basis of probability theory. #Poetry #Science #History #Mathematics #ProbabilityTheory #Pascal #Fermat (https://sharpgiving.com/thebookofscience/items/p1654.html)

1In 1654, letters between Blaise Pascal and Pierre de Fermat established the basis of probability theory. #Science #History #Poetry #Mathematics #ProbabilityTheory (https://sharpgiving.com/thebookofscience/items/p1654.html)

@pgrepds I thought I coudn't understand #probability.
Thanks to a teacher, I understand better the relationship between #probabilitytheory, #settheory and #topology. Now, I think I will be able to work these different fields together.

I get an extra layer of humor here by being amongst the LessWrong crowd...

#Peanuts #Lucy #CharlieBrown #Odds #NeverTellMeTheOdds #LessWrong #Rationality #Rationalism #ProbabilityTheory