THE EXPERT EDGE BY ZPONZ: Expert in Topology
Whitefoot’s research advances the theoretical foundations and computational modeling of engineering design and technology change in the context of market and regulatory systems to inform product development, manufacturing, and policymaking
#ZPONZ #GetPaidForExpertise #MonetizeYourSkills #Topology

“I’m not going to attempt to draw this object [a 3-torus] as this is not an object that fits in three dimensional space.”

Ace video from Quanta Magazine about 4 dimensional geometry.

13-minute video: https://youtu.be/MURzTFRRuJQ

#Maths #Math #Geometry #Topology

Effective Task Scheduling based on Candidate Optimization Algorithm (COA) in Heterogeneous NoC-Based MPSoC.
#Jenetics #GeneticAlgorithm #Costs #PowerDemand #NetworkTopology #SchedulingAlgorithms #Switches #Scheduling #TimeMeasurement #Topology #IPNetworks #Optimization
https://ieeexplore.ieee.org/abstract/document/11019139

#math #physics #quantum #tqft #qft #topology #logic

https://www.authorea.com/users/854182/articles/1302444-diagnosing-contextuality-in-a-topological-quantum-field-theory-a-toy-model

I will be writing about learning #topology via #logic and #categorytheory

First, some resources:

Tai-Danae Bradley, Tyler Bryson, and John Terilla:
https://topology.mitpress.mit.edu/

Vickers: https://archive.org/details/topologyvialogic0000stev/page/210/mode/1up (not free)

Amity Aharoni Rodrigo Nicolau Almeida Søren Brinck Knudstorp : https://knudstorp.github.io/pdfs/Lecture%20notes,%20Introduction%20to%20Topology%20in%20and%20via%20Logic.pdf

#TopologyViaLogic

A Concise Course in Algebraic Topology (Chicago Lectures in Mathematics) 1st Edition by J. P. May (PDF)
Author: J. P. May
File Type: PDF
Download at https://sci-books.com/a-concise-course-in-algebraic-topology-chicago-lectures-in-mathematics-1st-edition-0226511839/
#Topology, #J.P.May

A First Course in Topology: An Introduction to Mathematical Thinking (Dover Books on Mathematics) by Robert A Conover (PDF)
Author: Robert A Conover
File Type: PDF
Download at https://sci-books.com/a-first-course-in-topology-an-introduction-to-mathematical-thinking-dover-books-on-mathematics-b00izuefty/
#Topology, #RobertAConover

Cohomology Operations and Applications in Homotopy Theory (Dover Books on Mathematics) by Robert E. Mosher (PDF)
Author: Robert E. Mosher
File Type: PDF
Download at https://sci-books.com/cohomology-operations-and-applications-in-homotopy-theory-dover-books-on-mathematics-0486466647/
#Topology, #RobertE.Mosher

Ah, yes, the classic tale where #AI geniuses discover that deep learning is just #topology in disguise 🤯. Because clearly, neural networks are just playdoh for the mathematically elite 🧠. Who knew all those AI breakthroughs were just arts and crafts for adults? 🎨👶
https://theahura.substack.com/p/deep-learning-is-applied-topology #DeepLearning #NeuralNetworks #MathHumor #TechTrends #HackerNews #ngated

Who is someone walking around with 24GB of RAM?

Someone with a desktop $25-60K #Cray supercomputer.

Cray CX1 specs
#24 GB RAM
24 core Xenon #cpu

likely #topology :
quad core 64bit (dual core, cpu0 cpu1) cpu [with 8GB RAM x 3] times 3 = 24
24 x 2 = 48
48 x 2 = upto 96 cores!

@Gammitin

Eta Products and Theta Series Identities (Springer Monographs in Mathematics) 2011th Edition by Gà¼nter Kà¶hler (PDF)
Author: Günter Köhler
File Type: PDF
Download at https://sci-books.com/eta-products-and-theta-series-identities-springer-monographs-in-mathematics-2011th-edition-3642161510/
#Topology, #GünterKöhler

How knitting can be used to map topological surfaces and the bonds between maths and knitting

(surprisingly accessible, even withtout any theoretical understanding of maths and topology)

#knitting #topology #maths

https://sites.math.rutgers.edu/~rlg131/topology_and_knitting.pdf

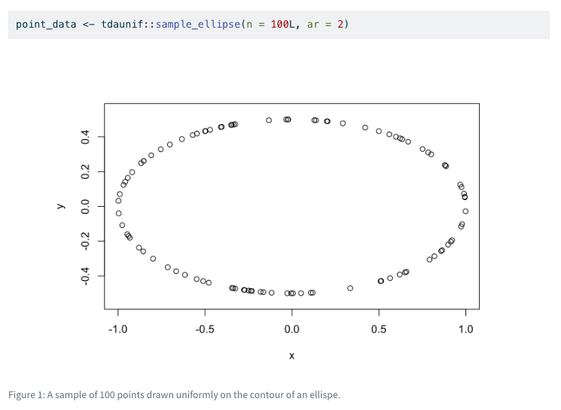
A unifying toolbox for handling persistence data - by Aymeric Stamm, Jason Cory Brunson

Topological data analysis (TDA) is a rapidly growing field that uses techniques from algebraic topology to analyze the shape and structure of data.

The {phutil} package provides a unified toolbox for handling persistence data. It offers consistent data structures and methods that work seamlessly with outputs from various TDA packages.

Find out more! https://r-consortium.org/posts/unifying-toolbox-for-handling-persistence-data/

#rstats #opensource #topology

On /r/math, someone asked about the motivation for the axioms of a topology. They are a bit mysterious. But this comment (https://www.reddit.com/r/math/comments/1km22kg/comment/ms72zz2/ ) was super insightful!

The idea is to capture notions of "closeness" and to be able to define continuous functions in a way that's 100% compatible with our usual real analysis definition of continuous function.

There's the classic "inverse of an open set is always open" definition, but that's equivalent to this one, which I think is far more intuitive, and also brings in our idea of closeness. From the comment:

Say that \(x\) "touches" a set \(A\) if \(x\) is in the closure of \(A\).

A continuous function is one for which, for any point \(x\) and set \(A\), if \(x\) touches \(A\), then \(f(x)\) touches \(f(A)\).

This is equivalent to the above inverse function definition; it avoids using the inverse function, and directly addresses our intuition: for continuous functions, two points in the domain that are close to each other are close in the codomain. Moving a tiny bit in the domain moves a tiny bit in the image.

Next step: invent time machine, go back to undergrad @ddrake studying topology, and tell him about this.

#math #topology

A century-old enigma, graph theory and design
Behind a static form, there are connections, transformations and, above all, the elegance of mathematics.

👉 Discover MORE and SUBSCRIBE to our summary of news and updates through link: https://amusementlogic.com/general-news/a-century-old-enigma-graph-theory-and-design/

📐 #graphtheory #mathematicaldesign #geometry #science #designscience #topology #computationaldesign #teoriadegrafos #diseñomatematico #geometria #ciencia #topologia #diseñocomputacional #sabiasque #saviezvousque #théoriedesgraphes

Do any of you know why in algebraic topology degeneracy maps are conventionally labelled with an s and face maps with a d?

#topology

A User's Guide to Operator Algebras 1st Edition by Peter A. Fillmore (PDF)
Author: Peter A. Fillmore
File Type: PDF
Download at https://sci-books.com/a-users-guide-to-operator-algebras-1st-edition-0471311359/
#Topology, #PeterA.Fillmore

Algebraic Topology: Homology and Cohomology (Dover Books on Mathematics) by Andrew H. Wallace (PDF)
Author: Andrew H. Wallace
File Type: PDF
Download at https://sci-books.com/algebraic-topology-homology-and-cohomology-dover-books-on-mathematics-0486462390/
#Topology, #AndrewH.Wallace