Lmst

Symmetrical waves of striped color with mandelbrot shapes and patterning

After two months of search for some errors in the linear approximation implementation, I *FINALLY* found that one typo, which caused bad images at deep zoom levels.

It's sooo much better now.

#Mandelbrot #Fractal #DearImGui #Programming

A GUI with coordinate parameters and an image of a deep Mandelbrot set zoom, which appears to be a stack of small rings. Right, a terminal, running the GUI program and sowing some progress.

#SelfPrivacy #mandelbrot #fractal by @mondstern #art #MastoArt

https://f-droid.org/packages/pro.kherel.selfprivacy/

@kirill

$SelfPrivacy mandelbrot fractal by mondstern$

Mandelbulb: The Unravelling of the Real 3D Mandelbrot Fractal
The original web page describing the development of a 3D equivalent to the Mandelbrot set.

#fractal #Mandelbrot #Mandelbulb

#Monday #Mandelbrot #MathArt #MondayMood

Candy-like embossed shiny spirals in bright colors

#Fractalfriday
I updated my #Shadertoy #fractal explorer. Link: https://www.shadertoy.com/view/33sSRf
It now supports skewing the C-plane using a quad of four draggable points. The coefficients 'a' and 'b' can now also changed by the mouse. To show the points, simply hold the space bar.

Here is a video which demonstrates that.
The formula is $z_{n+1}=z_n^2*\frac{z_n-a}{z_n-b}+c$
where a and b are the blue points in the video.

#Mathart #GLSL #Mandelbrot #creativecoding

Not really an example of #photography today. #math is more like it:

https://adam-gladstone.pixels.com/featured/mathematica-adam-gladstone.html

#mandelbrotset #mandelbrot #buyintoart #ayearforart #mathematics #maths

These turned out quite nice, I think. Guess I need a 4k monitor now. 🚀

Full res PNGs (~45 MB total): https://movq.de/v/fa024865a8/

#Mandelbrot

Some parts of the Mandelbrot set look like embedded Julia sets and this is one of them. Almost symmetrical, elliptic. Horizontal and vertical antennas. Trans color scheme.

🌋 #Monday #Math #Mandelbrot #Mood

plasma eruptions in glowing red and white

The trans, ace, and aro colors make for some nice #Mandelbrot palettes.

Full res PNGs (~90 MB total): https://movq.de/v/c732f4178a/

#Monday #Mandelbrot #MathArt #MondayMood

Fractal tendrils and spirals in glowing red-yellow with electric blue energy waves

Icosagon fractal

$ z_{n+1}=fold(z_n)^2+c $
with 10 folds total.

Colors produced by blending multiple color gradients of escape time, distance estimation, atom domain, phase and triangle inequality average together.

#fractal #fractalart #mathart #mandelbrot #algorithmicart #creativecoding #shadertoy #glsl

$Rainbow colored detailed fractal "ring" with a lot of star like patterns.$

Frame by Frame #Monday #Mandelbrot #MathArt #MondayMotivation

Fractal paisley blobs in muted red to purple gradients

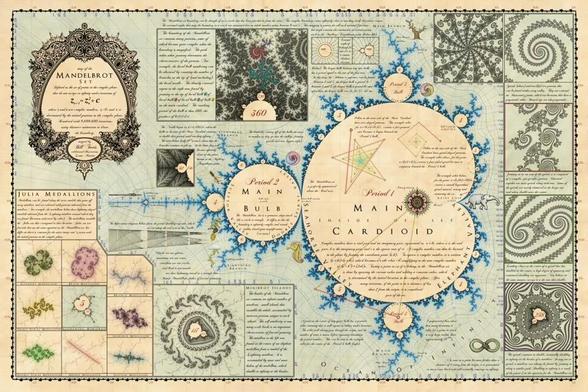
Vintage-Style Map of the Mandelbrot Set via Kottke [Shared]

Bill Tavis designed this lovely vintage-style map of the familiar fractal shape, the Mandelbrot set. He is selling a poster version of the map, starting at the very reasonable price of $24. I don’t usually highlight the price on this sort of thing, but an unauthorized seller on Amazon was selling poor-quality counterfeits of the map and even though it wasn’t his fault, Tavis offered to replace any of the crappy maps for free. Great map, and apparently a great human who made it.

https://welchwrite.com/blog/2025/04/26/vintage-style-map-of-the-mandelbrot-set-via-kottke-shared/

#math #mathematics #fractals #chaos #mandelbrot #map #poster #shared

$The image is a detailed and artistic representation of the Mandelbrot Set, a famous fractal in mathematics. The overall layout resembles a map, with various sections and labels. The central focus is the "Main Cardioid," a heart-shaped region, surrounded by intricate blue fractal patterns. The "Period 1 Main Bulb" and "Period 2 Main Bulb" are labeled, indicating different parts of the set. The image includes smaller sections labeled "Julia Medallions," showcasing various Julia sets, which are related to the Mandelbrot Set. The background features a light beige color with ornate borders and decorative elements, enhancing the vintage aesthetic. Textual elements, such as "Mandelbrot Set" and "Julia Medallions," are present, along with mathematical notations and descriptions. The image combines scientific information with artistic design, creating a visually engaging representation of complex mathematical concepts. Provided by @altbot, generated privately and locally using Ovis2-8B$

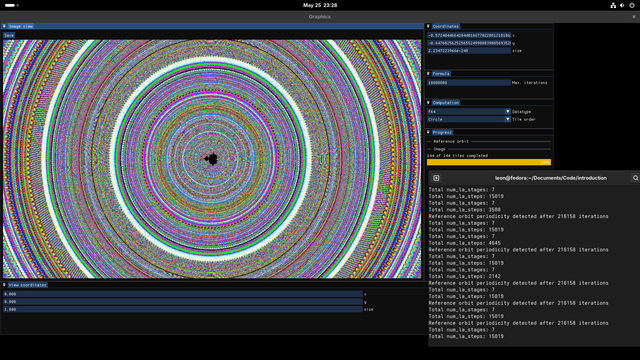
I've released the first version of complexitty: a simple #Mandelbrot set explorer for the #terminal -- it's the successor and replacement for `textual-mandelbrot`. More features to come.

https://blog.davep.org/2025/04/20/complexitty.html

#python #programming #textual

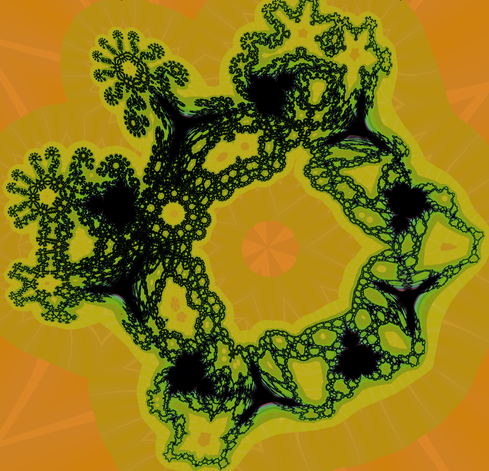
Decagon (fractal version)

$z_{n+1}=fold(z_n)^2+c$

where fold is a generalized absolute value function. A complex number has two components: a real and an imaginary part.
If we take the absolute value of one of these parts, we can interpret this as a fold in the complex plane. For example, |re(z)| causes a fold of the complex plane around the imaginary axis, which means that the left half ends up on the right half. If we do this for the imaginary component |im(z)|, we fold the complex plane around the real axis which means that the bottom half ends up on the top half.
These two operations are quite similar, because the imaginary fold is just like the real fold of the plane, except that it was previously rotated 90 degrees (z * i). But what if we rotate the plane by an arbitrary number of degrees?
An arbitrary rotation of the complex plane can be expressed as rot(z, radians) = z * (cos(radians) + sin(radians) * i), where radians encodes the rotation.

The image here is produced, by rotating the plane exactly five times, and folding the imaginary part each time.

I found this algorithm in the Fractal Formus under the name “Correction for the Infinite Burning Ship Fractal Algorithm”.
It can be seen as a generalization of the burning ship obtained by folding the complex plane twice with a rotation of 90 degrees, i.e. folding both the real and the imaginary part.

#fractalfriday #fractal #burningship #mandelbrot #complexplane #complexnumbers #mathart #math #escapetimefractals

$Black fractal structures on a mostly green background, rendered using distance estimation.$

Die Folien und Ressourcen für meinen #Mandelbrot-Workshop auf dem #Easterhegg heute findet Ihr übrigens hier:

https://codeberg.org/Piko/Mandelbrot-Workshop

#eh22

"Lindenmayer Systems, Fractals, and Plants" (PRUSINKIEWICZ; HANAN, 1989) https://link.springer.com/book/10.1007/978-1-4757-1428-9

#LSystem #Fractals #Mandelbrot #ComputationalBiology

$Preface L-systems are a mathematical formalism which was proposed by Aristid Lindenmayer in 1968 as a foundation for an axiomatic theory of development. The notion promptly attracted the attention of computer scientists, who investigated L-systems from the viewpoint of formal language theory. This theoretical line of research was pursued very actively in the seventies, resulting in over one thousand publications. A different research direction was taken in 1984 by Alvy Ray Smith, who proposed L-systems as a tool for synthesizing realistic images of plants and pointed out the relationship between L-systems and the concept of fractals introduced by Benoit Mandelbrot. The work by Smith inspired our studies of the application of L-systems to computer graphics. Originally, we were interested in two problems: • Can L-systems be used as a realistic model of plant species found in nature? • Can L-systems be applied to generate images of a wide class of fractals? It turned out that both questions had affirmative answers. Subsequently we found that L-systems could be applied to other areas, such as the generation of tilings, reproduction of a geometric art form from East India, and synthesis of musical scores based on an interpretation of fractals. This book collects our results related to the graphical applications of 1systems. It is a corrected version of the notes which we prepared for the ACM SIGGRAPH '88 course on fractals. [...]$