On the Arnold diffusion mechanism in Medium Earth Orbit, now in Journal of Nonlinear Science from our colleague M. Guardia and I. Baldomà and their collaborators E.M. Alessi and M. Giralt.
Check it out here to learn more:
https://link.springer.com/article/10.1007/s00332-024-10080-0
On Nested Central Configurations of the 3n Body Problem, now in Nonlinear Science from our colleague J.M. Cors and his collaborators E. Barrabés, A. C. Fernandes and C. Vidal.
Check it out here to learn more:
https://link.springer.com/article/10.1007/s00332-025-10162-7
Oscillatory Motions, Parabolic Orbits and Collision Orbits in the Planar Circular Restricted Three-Body Problem, now in Communications in Mathematical Physics from our colleagues José Lamas, Marcel Guardia and Tere M. Seara
Check it out here to learn more
https://link.springer.com/article/10.1007/s00220-025-05283-9
The IMTECH Newslater is live.
You can find there two enlightening interviews to our colleagues T. Guillemon and V. Mañosa.
Also J. Curbelo presented a very nice outreach article about fluid Dynamics.
You can find it: https://imtech.webs.upc.edu/2025/01/01/newsletter-07-january-december-2024/
I'd forgotten what a great concept phase space is! This plot of the state of a pendulum over time is delightful. Play around with it for yourself: openprocessing.org/sketch/1989770 #maths #physics #dynamicalSystems
On small breather of nonlinear Klein-Gordon equations via exponentially small homoclinic splitting, now in Inventiones mathematicae from our colleagues T. M. Seara and M. Guarda and their co-workers O. M.L. Gomide and C. Zeng..
Check it out here to learn more: https://link.springer.com/article/10.1007/s00222-025-01327-y
Are you a graduate student or postdoc who wants to add novel developmental biology and biophysics methods to your research? Then have a look at #EMBLDevBio, where you'll learn all about highly multiplexed RNA fluorescent in situ hybridisation, quantitative imaging and analysis, machine learning based image segmentation, and more 🥼👀
📥 Apply by 26 March 2025
🔗 https://s.embl.org/ptd25-01-ma
🗺️ EMBL Heidelberg
📅 2 – 9 July 2025
(10/n) If you’ve made it this far, you’ll definitely want to check out the full paper. Grab your copy here:
https://www.biorxiv.org/content/10.1101/2024.12.17.628339v1
📤 Sharing is highly appreciated!
#compneuro #neuroscience #NeuroAI #dynamicalsystems
Our colleague Jezabel Curbelo is organizing the 4th NonLinear processes in Oceanic and Atmospheric flows at the Institut de Ciencies del Mar (Barcelona, Spain) from January 22nd to January 24th:
NLOA 2025 intends to create cross-disciplinary interaction among mathematicians, physicists, oceanographers and atmospheric scientists in a wide sense. It will focus on nonlinear dynamics of atmospheric and oceanic phenomena, and it aims to create an international forum where international researchers explore timely open problems in ocean and atmosphere sciences, and also investigate the power and impact of mathematics in these areas.
Registration Deadline till January 8th.
More info: https://www.crm.cat/4th-nonlinear-processes-in-oceanic-and-atmospheric-flows/
#appliedMath #DynamicalSystems #Interdisciplinarity #MathEverywhere
From April 27th to May 2nd we will be present at #EGU25 in the session organized by Jezabel Curbelo about Lagrangian perspectives on transport and mixing in geophysical fluids:
We invite presentations on topics including – but not limited to – the following:
- Large-scale circulation studies using direct Lagrangian modeling and/or age and chemical tracers (jets, gyres, overturning circulations);
- Exchanges between reservoirs and mixing studies (e.g. transport barriers and Lagrangian Coherent Structures in the stratosphere and in the ocean, stratosphere-troposphere exchange);
- Tracking long-range anthropogenic and natural influence (e.g. effects of recent volcanic eruptions and wildfire smoke plumes on the composition, chemistry, and dynamics of the atmosphere, transport of pollutants, dusts, aerosols, plastics, and fluid parcels in general, etc);
- Inverse modeling techniques for the assessment and constraint of emission sources (e.g. backtracking, including diffusion and buoyancy);
- Model and tool development, computational advances.
Find us at https://meetingorganizer.copernicus.org/EGU25/session/52516
#dynamicalSystems #AppliedMath #mathInGeosciences #Interdisciplinary
The 2024. #Barcelona #DynamicalSystems #Prize has been awarded to Massimiliano Berti, Alberto Maspero i Paolo Ventura, authors of the article “Full description of Benjamin-Feir instability of Stokes waves in deep water“, Invent. Math.
230 (2022), no. 2, 651–711. Read the full announcement from @SCM https://scm.iec.cat/eng/massimiliano-berti-alberto-maspero-i-paolo-ventura-barcelona-dynamical-systems-prize/
21st School on Interactions between #DynamicalSystems and #PartialDifferentialEquations
📅 June 30 - July 04, 2025
📍Centre de Recerca Matemàtica (Barcelona)
Registration is open.
⚠️ Registration deadline is June 12, 2025.
The registration fee (200€/75€ for granted) includes coffee breaks and lunch.
⚠️ Application deadline for grants and posters is April 13th, 2025.
The School on Interactions between Dynamical Systems and Partial Differential Equations (JISD) is an annual international summer school consisting of four short courses of around five hours given by four world-leading experts.
LECTURERS
Dmitry Dolgopyat | University of Maryland
Serena Dipierro | University of Western Australia
Luciano Mari | Università di Torino
Sylvain Crovisier | Université Paris-Saclay
Everyone knows about synchronization in chaotic systems. But what happens when one studies the synchronizability of periodic ones? Two main things.
The first is that new classes of synchronization stability emerge that are characteristic of periodic systems and are not found in chaotic ones. The root cause of this is that the master stability function of periodic systems is 0 at the origin, in difference to what happens in chaotic systems, for which it is strictly positive.
The second thing is that we challenge the long-held belief that periodic systems synchronize in a stable way for any coupling, no matter how small. In fact, we show that many of them, for many coupling schemes, have a non-zero lower threshold for synchronization stability.
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.6.043105
#physics #mathematics #networks #complexsystems #chaos #dynamicalsystems #synchronization #complexity #stability
Symbolic dynamics builds a bridge from #DynamicalSystems to computation/ #AI!
In our #NeurIPS2024 (@NeurIPSConf) paper we present a new network architecture, Almost-Linear RNNs (Fig. 1), that finds most parsimonious piecewise-linear representations of DS from data:
https://arxiv.org/abs/2410.14240
These representations are topologically minimal (Fig. 5,7), profoundly easing interpretation and math. analysis of the underlying data-generating DS.
The AL-RNN furthermore naturally gives rise to a symbolic encoding that provably preserves important topological properties of the underlying dynamical system.
Symbolic dynamics directly links up with computational graphs, finite state machines, formal languages etc. (Fig. 2).
Spearheaded by Manuel Brenner and Christoph Hemmer, jointly with Zahra Monfared.
Interested in interpretable #AI foundation models for #DynamicalSystems reconstruction?
In a new paper we move into this direction, training common latent DSR models with system-specific features on data from multiple different dynamical regimes and DS: https://arxiv.org/pdf/2410.04814
(Fig. 7)
We show applications like transfer & few-shot learning, but most interestingly perhaps, subject/system-specific features were often linearly related to control parameters of the underlying dynamical system trained on …
(Fig. 4)
This gives rise to an interpretable latent feature space, in which datasets with similar dynamics cluster. Intriguingly, this clustering according to *dynamical systems features* led to much better separation of groups than could be achieved by more traditional time series features.
(Fig. 6)
Fantastic work by the incomparable Manuel Brenner and Elias Weber, together with Georgia Koppe!
Final call for the Modellers Workshop for the #BrainDynamicsToolbox. An online course for simulating custom #DynamicalSystems in #Neuroscience. It covers practical programming techniques for the major classes of #DifferentialEquations in #ComputationalNeuroscience. Example code is provided in all cases. Study time is 8 hours.
Course Website
https://bdtoolbox.teachable.com/p/modellers-workshop
Toolbox Website
https://bdtoolbox.org
Important Dates
Enrolments close 31st Aug 2024.
Yesterday, I posted an image of the #LorenzAttractor showing the evolution of three trajectories (shown in red, green and blue) starting close together. Here, I’ve made it into a little animation to show how the paths initially stay close to each other but after about a quarter of the duration plotted, they #diverge from each other irrevocably (i.e. become uncorrelated) but remain part of the #ChaoticAttractor.
#DynamicalSystems #Mathematics #AppliedMathematics #CCBYSA #FreeSoftware #WxMaxima
Just messing about a bit. Here is the famous #LorenzAttractor plotted using #WxMaxima. The three #trajectories, shown in red, green and blue are for three fairly nearby #InitialConditions.
#DynamicalSystems #ChaoticAttractors #StrangeAttractors #NumericalSolutions #Mathematics #AppliedMathematics #CCBYSA #FreeSoftware
Random generalized Lotka–Volterra model (Ecology 🏞️)
The random generalized Lotka–Volterra model is an ecological model and random set of coupled ordinary differential equations where the parameters of the generalized Lotka–Volterra equation are sampled from a probability distribution, analogously to quenched ...
https://en.wikipedia.org/wiki/Random_generalized_Lotka–Volterra_model
#RandomGeneralizedLotkaVolterraModel #Ecology #Biophysics #CommunityEcology #DynamicalSystems #PopulationEcology
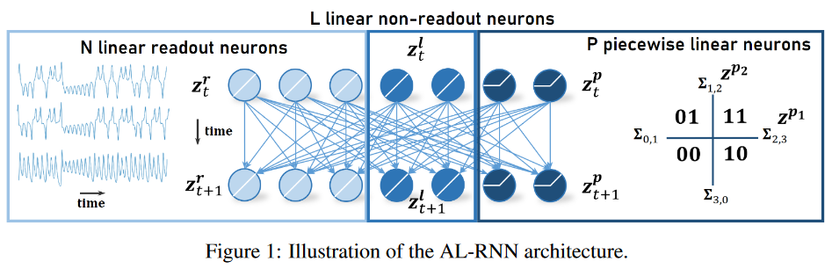
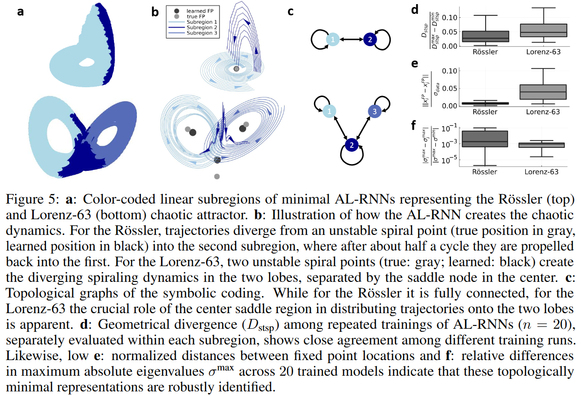
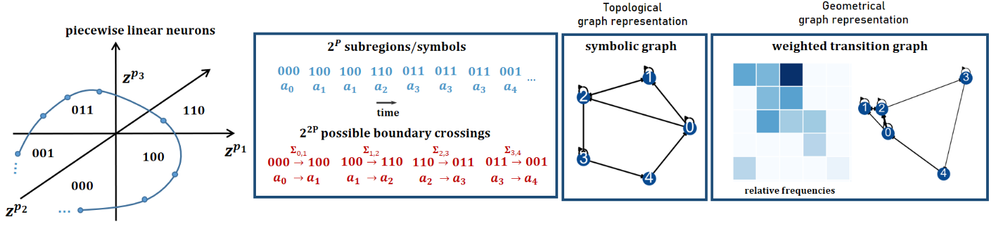
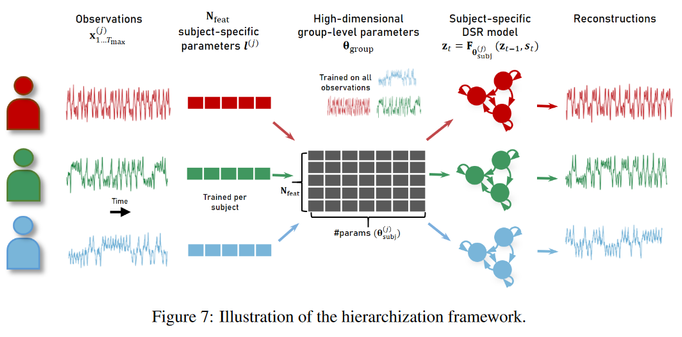
Magnitude-based pruning is a standard #ML #AI technique to produce sparse models, but in our @ICMLConf paper https://www.arxiv.org/abs/2406.04934 we find it doesn’t work for #DynamicalSystems reconstruction.
Instead, via geometry-based pruning we find the *network topology* is far more important!
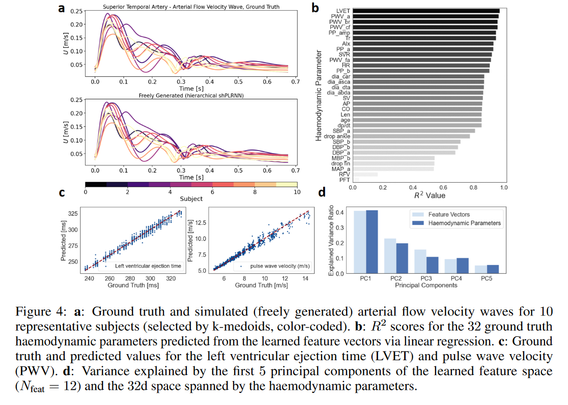
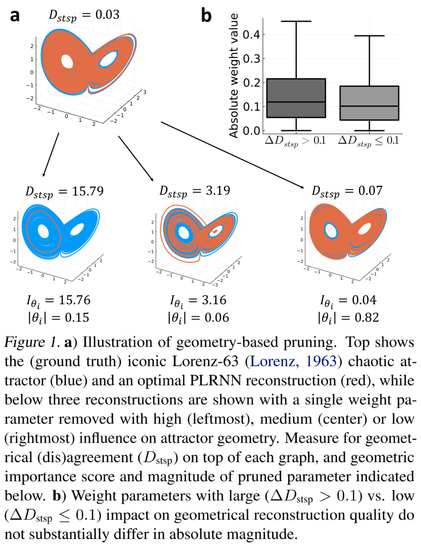
It turns out that even RNN weights small in relative size can have a dramatic impact on system dynamics as measured by attractor agreement. In fact, there is not much difference between small and large magnitude weights in contribution to DS reconstruction quality. (Fig. 1)
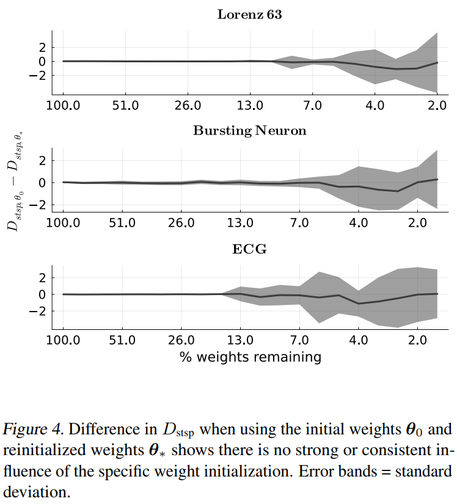
Following the lottery ticket hypothesis, we find that large RNNs still contain winning tickets that can be carved out by *geometry-based* pruning, but that these tickets are defined by *graph topology* with initial weight values hardly playing any role. (Fig. 4)
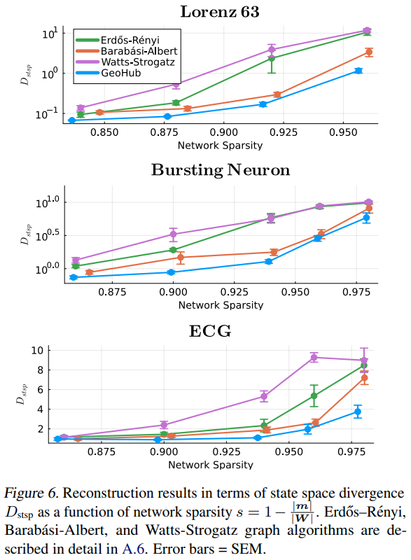
The ‘winning’ graph topology distilled from trained RNNs turns out to exhibit both hub-like and small world features. RNNs initialized with this topology perform significantly better than equally-sized RNNs with random, Watts-Strogatz or Barabási-Albert topology. (Fig. 6)
… and also train much faster. (Fig. 7)
This all makes sense: Natural and engineered DS often bear a specific sparse network topology that is crucial for shaping their dynamics!
Fantastic work lead by Christoph Hemmer with Manuel Brenner and Florian Hess!
