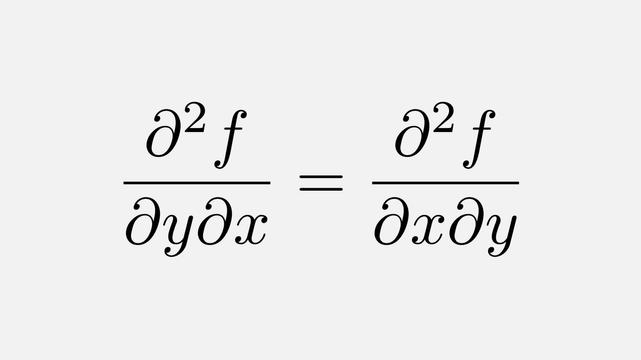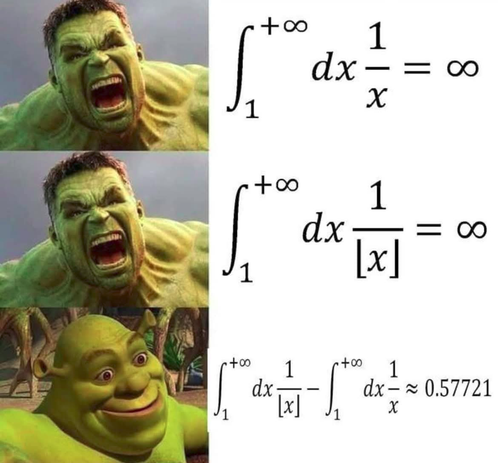Of course this was known to many famous #mathematicians, like #Euler and #Jacobi and they solved the equations in terms of #EllipticIntegrals. I find it satisfying to be able to visualize the #dynamics of the this system, using #FreeSoftware, such as #WxMaxima.

USM really does slash the rote burden, chiefly because one handful of exponential/hyperbolic identities replaces a patchwork of separate trig, inverse-trig, radical and Euler recipes.

Article (draft): https://arxiv.org/abs/2505.03754

#math #calculus #integral #new #euler #arxiv #halfangleapproach #symmetrymatters

I love LLMs, so much fun...😂 🤣 🤣
(The number e is a mathematical constant approximately equal to 2.71828 that is the base of the natural logarithm and exponential function. )

#mathematics #google #LLM #gemma3 #Euler

#KnowledgeBit: Leonhard #Euler is widely considered to be the most prolific mathematician; his 866 publications as well as his correspondences are being collected in the Opera Omnia Leonhard Euler which, when completed, will consist of 81 quarto volumes.

Carl Friedrich Gauss said that studying his work is still the best way to learn mathematics. Much of Euler's work was produced in the last 20 years of his life, when he was blind.

https://knowledgezone.co.in/kbits/664078e1795fa76928e0f922

@linuxgal
Euclid and "Oyler" need to get together and standardise their desired pronunciation, or we shall keep having this problem.

#math #maths #mathematics #english #greek #linguistics #language #names #euler #euclid

Un nuevo #modelo #matemático basado en las #ecuaciones de #Euler revela cómo mejorar una afición que gana adeptos en #España: la importancia de la #geometría y la #física en el lanzamiento de los #bolos

https://www.muyinteresante.com/ciencia/ecuaciones-euler-bolos-precision.html

Un nuevo #modelo #matemático basado en las #ecuaciones de #Euler revela cómo mejorar una afición que gana adeptos en #España: la importancia de la #geometría y la #física en el lanzamiento de los #bolos www.muyinteresante.com/ciencia/ecua...

Un nuevo modelo matemático bas...

One day, one decomposition
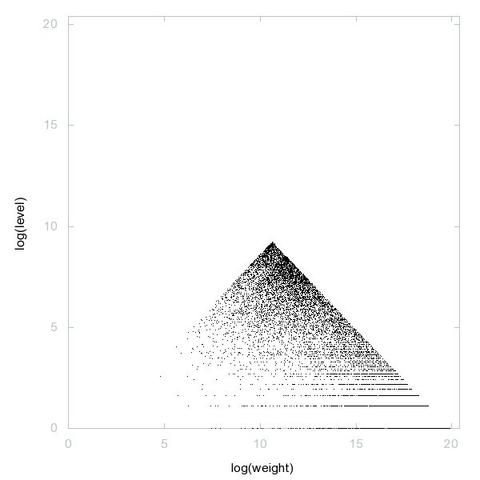
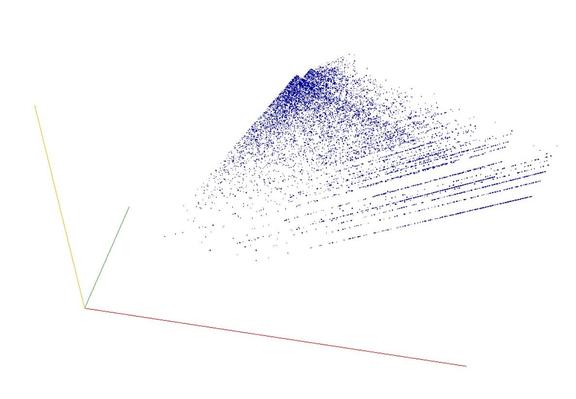
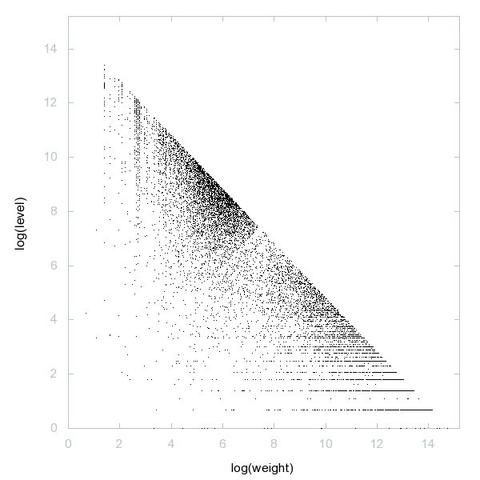
A228183: Semiprimes generated by the Euler polynomial x^2 + x + 41

3D graph, threejs - webGL ➡️ https://decompwlj.com/3Dgraph/A228183.html
2D graph, first 500 terms ➡️ https://decompwlj.com/2Dgraph500terms/A228183.html

#decompwlj #math #mathematics #sequence #OEIS #javascript #php #3D #numbers #semiprimes #Euler #polynomial #graph #threejs #webGL

One day, one decomposition
A217139: Numbers n such that phi(n) = phi(n+12), with Euler's totient function phi = A000010

3D graph, threejs - webGL ➡️ https://decompwlj.com/3Dgraph/A217139.html
2D graph, first 500 terms ➡️ https://decompwlj.com/2Dgraph500terms/A217139.html

#decompwlj #math #mathematics #sequence #OEIS #javascript #php #3D #numbers #Euler #totient #function #phi #graph #threejs #webGL

The USM, the Dominican method 🇩🇴, has relegated Euler substitutions to mere historical relics. Modern integration has a new name.

Method draft: https://drive.google.com/file/d/12DayP6cD1VwDIZCL-nMlcaNH2XUwHfAy/view?usp=drivesdk
#math #calculus #integrals #method #euler #halfangleapproach #symmetrymatters

#TrolleyProblem #Königsberg #Euler #maths #mathematics #math

Pi day grows near. The circumference of a circle divided by its diameters times the Euler's number e, also known as Napier's constant, gives us pie.
#pi #e #day #Euler #Napier

Ich glaube ich habe gerade eine Eulersche Scheibe in meiner Spülmaschine entdeckt #Physik #Euler #Rotation #Kreisel #Präzession

For the first time, the interchangeability of partial derivatives was proven by Leonhard Euler. #mathematics #calculus #euler #partialdifferentialequations

One day, one decomposition
A179188: Numbers n such that phi(n) = phi(n+6), with Euler's totient function phi=A000010

3D graph, threejs - webGL ➡️ https://decompwlj.com/3Dgraph/A179188.html
2D graph, first 500 terms ➡️ https://decompwlj.com/2Dgraph500terms/A179188.html

#decompwlj #math #mathematics #sequence #OEIS #javascript #php #3D #numbers #Euler #totient #function #graph #threejs #webGL

One day, one decomposition
A179186: Numbers n such that phi(n) = phi(n+4), with Euler's totient function phi=A000010

3D graph, threejs - webGL ➡️ https://decompwlj.com/3Dgraph/A179186.html
2D graph, first 500 terms ➡️ https://decompwlj.com/2Dgraph500terms/A179186.html

#decompwlj #math #mathematics #sequence #OEIS #javascript #php #3D #numbers #Euler #totient #function #graph #threejs #webGL

Euler–Mascheroni constant! :euler:

In fact, the last one is:
\[\large\displaystyle\int_1^{+\infty}\mathrm dx\ \left(\frac{1}{\lfloor x\rfloor}-\frac1x\right)=\gamma\approx0.5772156649\]

Equivalently,
\[\large\displaystyle\lim_{n\to\infty}\left(\sum_{k=1}^n \frac1{k}-\ln n\right)=\gamma=0.5772156649\ldots\]
---------------------------------------------------------------------------------------------------------------------
Unsolved problem in mathematics:
Is Euler–Mascheroni constant irrational? If so, is it transcendental?

#Euler #Mascheroni #EulerMascheroni #Constant #gamma #EulerConstant #EulersConstant #EulerMascheroniConstant #Irrational #Irrationality #Transcendental #Transcendence #Unsolved #UnsolvedProblem #Maths #Mathematics #Indeterminate #IndeterminateForm #IndeterminateForms #Inf #Infinity #HarmonicNumber #HarmonicNumbers #HarmonicSeries #Logarithm #Log #Logarithms #NaturalLogarithm #Integral #ImproperIntegral

Zum #TagDerEulerischenZahl

#KätToon #EulerischeZahl #Euler #Eule

The #Euclid-#Euler #Theorem is a fundamental theorem in #NumberTheory that beautifully connects #PerfectNumbers with #Mersenne #Primes.

https://knowledgezone.co.in/kbits/679340ac379a5d09cb2d1a93

𝐁𝐢𝐠 𝐔𝐩𝐝𝐚𝐭𝐞 𝐨𝐧 𝐌𝐲 𝐈𝐧𝐭𝐞𝐠𝐫𝐚𝐭𝐢𝐨𝐧 𝐓𝐞𝐜𝐡𝐧𝐢𝐪𝐮𝐞!

I'm excited to share the latest development in what I initially called the "Exponential Substitution Method." Moving forward, this approach will be known as the Unified Substitution Method because it unifies several powerful techniques for tackling integrals, including:

𝟏. 𝐂𝐨𝐦𝐩𝐥𝐞𝐱 𝐄𝐱𝐩𝐨𝐧𝐞𝐧𝐭𝐢𝐚𝐥𝐬 𝐟𝐨𝐫 𝐓𝐫𝐢𝐠𝐨𝐧𝐨𝐦𝐞𝐭𝐫𝐢𝐜 𝐅𝐮𝐧𝐜𝐭𝐢𝐨𝐧𝐬: Originally used to simplify integrals by expressing sine and cosine in terms of exponential functions, this technique is extended to handle irrational integrands.

𝟐. 𝐖𝐞𝐢𝐞𝐫𝐬𝐭𝐫𝐚𝐬𝐬 𝐒𝐮𝐛𝐬𝐭𝐢𝐭𝐮𝐭𝐢𝐨𝐧: Traditionally used to transform rational expressions of trigonometric functions into purely rational ones, this is now extended and incorporated into my method to simplify irrational expressions as well.

𝟑. 𝐄𝐮𝐥𝐞𝐫 𝐒𝐮𝐛𝐬𝐭𝐢𝐭𝐮𝐭𝐢𝐨𝐧𝐬: These classic substitutions, designed for certain irrational integrands, are also integrated into the Unified Substitution Method. Interestingly, I’ve found that the extended Weierstrass substitution often simplifies integrals into rational forms nearly identical to those obtained through Euler’s substitutions.

By unifying and extending these techniques, this method becomes a comprehensive tool capable of handling a wide variety of integrals, including some of the most challenging irrational ones.

This approach represents a significant step forward in simplifying integral calculus and demonstrates the deep interconnections between these classic methods. I’m excited to see how this can benefit students, researchers, and enthusiasts alike.

To stay tuned for more examples and demonstrations of this method, here is my blog post on it:

https://geometriadominicana.blogspot.com/2024/03/integration-using-some-euler-like.html?m=1

#math #calculus #integration #euler #weierstrass #new #method