I'm a sucker for non-euclidian visualizations. Gave myself a headache the day hyperbolica released but it was worth it. From the dev of #HyperRogue
#nonEuclideanGeometry
An aperiodic tessellation of the hyperbolic plane, found by Toimine in the #tessellations channel in the HyperRogue discord.
These tiles are equilateral, with edge length of 0.56358, which is less than the 0.56626 that was achieved by the regular {7,3} tiling (which was apparently the previous record for a tiling with equilateral convex tiles).
It is also possible to the connect two pentagons by their "bases" to obtain a funky variant of the {8,3} tiling. Then, we can play with the angles -- for "narrow" tiles, the edge length becomes even smaller, about 0.5436.
The animated visualization also shows some new cool features of the RogueViz expression parser: it can now automatically solve for the edge length which makes the tiling work for the given angle \(\alpha\)!
https://github.com/zenorogue/hyperrogue/blob/master/tessellations/sample/aperiodic_pentagons.tes
A monster kills a monster, only to be killed by another monster, and somehow, there are enough monsters for every monster to kill forever.
Higher Geometry by N. V. Efimov
This book gives a systematic presentation of the fundamentals of Euclidean geometry, non-Euclidean geometry of Lobachevsky and Riemann, projective geometry and the geometrical aspects of special relativity theory. It also gives a general idea about constant curvature geometries. The subject matter has been shaped by the needs of the students and by my own experience.
A few words on the use of the book as a textbook in a course of the foundations of geometry are in order. The subject matter is distributed over the first two parts. It is presented systematically throughout the book and practically does not omit any of the details of the arguments (except for the proofs of certain theorems of elementary geometry). It is evident that in lectures such a detailed presentation would be unprofitable (even if many hours were assigned to this course). The most difficult portion is Chapter 2 in the first part of the book; I feel that in lectures one should discuss from this chapter the formulations of the axioms and present examples of rigorous proofs of certain theorems; moreover, the most important aspects, for example, the measurement of length, the equivalence of Archimedes’ and Cantor’s axioms to Dedekind’s axiom and the significance of these axioms for the substantiation of analytic geometry, should be discussed in detail. The proof of the majority of the initial theorems of elementary geometry should be left for self-study.
Translated from the Russian by P. C. Sinha, Cand.Sc.
You can get the book here and here
Contents
Preface to the English Edition 9
Part 1. The Foundations of Geometry
A Short Review of Investigations into the Foundations of Geometry
1.1 Euclid’s definitions, postulates, and axioms
1.2 The fifth postulate 16
1.3 Lobachevsky and his geometry 33
1.4 The formation of the notion of geometrical space 36
The Axioms of Elementary Geometry
2.1 Geometrical elements 42
2.2 Group I: axioms of incidence 42
2.3 Group II: axioms of betweenness 45
2.4 Corollaries of the axioms of incidence and betweenness 45
2.5 Group III: axioms of congruence 53
2.6 Corollaries of Axioms I-III 57
2.7 Group IV: axioms of continuity 69
2.8 Group V: the axiom of parallelism. Absolute and divergent lines 96
Chapter 3. The Non-Euclidean Theory of Parallels
3.1 Lobachevsky’s definition of parallels 82
3.2 Peculiarities in the location of parallel lines 85
3.3 Lobachevsky’s function II(x) 100
3.4 Lines and planes in Lobachevskian space 104
3.5 Equidistants and oricycles 111
3.6 Equidistant surfaces and horospheres 121
3.7 Elementary geometry on surfaces in Lobachevskian space 126
3.8 Area of a triangle 136
3.9 Proof of logical consistency of Lobachevskian geometry 146
3.10 The basic metric relationships in Lobachevskian geometry 165
3.11 Riemannian geometry: a brief survey 178
Chapter 4. Investigation of the Axioms of Elementary Geometry
4.1 Three basic problems of axiomatic theory 188
4.2 Consistency of the axioms of Euclidean geometry 191
4.3 Proof of independence of some axioms of Euclidean geometry 205
4.4 Axiom of completeness 216
4.5 The completeness of axioms of Euclidean geometry 220
4.6 The axiomatic method in mathematics
Part 2. Projective Geometry
Chapter 5. The Foundations of Projective Geometry
5.1 The subject matter of projective geometry 223
5.2 Desargues’ theorem. Harmonic sets of elements 226
5.3 Order of points on the projective line 231
5.4 Division of harmonic pairs. Continuity of the harmonic correspondence 244
5.5 The axiom of continuity. Projective system of coordinates on a line 252
5.6 Projective coordinate systems on a plane and in space 258
5.7 Projective correspondence between elements of one-dimensional manifolds 270
5.8 Projective correspondences between two- and three-dimensional manifolds 283
5.9 Analytic representation for projectivities. Involution 292
5.10 Transformation formulas for projective coordinates. Cross ratio of four elements 300
5.11 The principle of duality 316
5.12 Algebraic curves and pencils. Algebraic surfaces and bundles. Complex projective plane and complex projective space 325
5.13 Images of second degree. The theory of polars 337
5.14 Constructive theorems and problems of projective geometry 346
Chapter 6. Group-Theoretic Principles in Geometry. Groups of Transformations
6.1 Geometry and the theory of groups 362
6.2 The projective group and its basic subgroups 391
6.3 Geometries of Lobachevsky, Riemann, and Euclid in the projective setting 408
Chapter 7. Minkowski Space
7.1 Multidimensional affine space 425
7.2 Euclidean spaces and Minkowski space 440
7.3 The space of events of the special relativity theory 455
Chapter 8. Differential Properties of Non-Euclidean Metric
8.1 Metric form of the Euclidean plane 474
8.2 The distance between two points on the Lobachevskian plane 478
8.3 Metric form of the Lobachevskian plane 489
8.4 Intrinsic geometry of a surface and the Beltrami problem 505
8.5 Geometry on a surface of constant curvature 511
8.6 Derivation of basic metric relations in Lobachevskian geometry 523
Part 3. Constant Curvature Geometry
Chapter 9. Spatial Forms in Constant Curvature Geometry
9.1 Two-dimensional manifolds with differential-geometric metric 529
9.2 Parabolic spatial forms 537
9.3 Elliptic spatial forms 544
9.4 Hyperbolic spatial forms 547
Name Index 553
Subject Index 554
#1980 #axioms #EuclideanGeometry #geometry #lobachevsky #mathematics #metricRelations #minkowskiSpace #nonEuclideanGeometry #parallelism #projectiveGeometry #riemannianGeometry #sovietLiterature
Our new video!
In most of our videos, we have been playing with the non-Euclidean spaces. However, we have not played with the time dimension in them so far. In this video, we will combine spherical and hyperbolic geometry with relativistic effects.
#RogueViz #RelativeHell #mathart #NonEuclideanGeometry #RelativitySpace
Do you want the hexes on a sphere to be regular?
Or do you want them to be of the same area?
Or do you want straight lines be actually straight? (in one of two ways)
And the same idea with squares.
The animation on the left shows clearly that the shortest path is the straight line. Unbelievably, there are possible worlds where this would NOT be the case!
For example, it is not true in Discworld from Terry Pratchett's novels, which is famously a flat world. In a flat world, the shortest path is NOT a straight line!
(Based on the map of Discworld from https://www.reddit.com/r/discworld/comments/odrog0/wip_discworld_high_res_map/ )
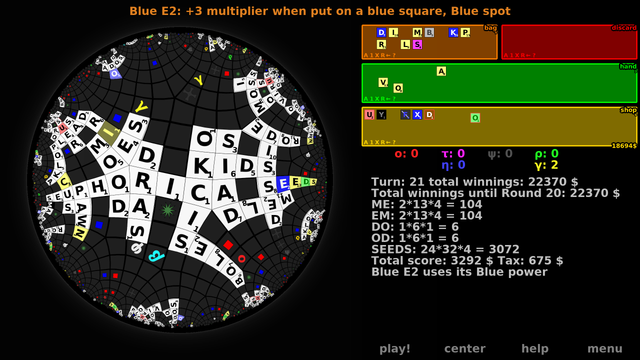
Ported Seuphorica (Scrabble solitaire deckbuilder) to RogueViz for a more intuitive and powerful interface!
(1) Infinite square grid, with standard Seuphorica special powers. Letters E and R (inverse colors close to the gigantic EE top left) are "reversing", hence "RE" is accepted and "EE" is accepted multiple times. Note the word GEESE which uses a portal to get a multiplier for gigantic 'E' two times in a single word. "PETER" uses a mirror.
But since this is RogueViz, let us make the board geometry abstract, to have even more fun with geometry and topology!
(2) Usually, words can only go "right" and "down". In hyperbolic geometry, we have holonomy, so "right" and "down" are not globally defined. So we have to accept both directions. (Or, optionally, only accept words if they are valid both ways.)
(3) In this one, "right" and "down" are not globally defined either, but "horizontal" and "vertical" are (in a somewhat twisted way), so Seuphorica "horizontal" and "vertical" multiplier powers can work.
Although the hexagons somehow turn a horizontal word into a vertical one...
#RogueViz #NonEuclideanGeometry #mathart #noneuclidean #HyperbolicGeometry #Seuphorica #scrabble
(to be continued...)
Developer's intention: A beautiful visualization feature!
What the users share: A chaotic art generator! BREAK THE LIMITS! 🎨🔥
#HyperRogue #RogueViz #HyperbolicGeometry #NonEuclideanGeometry #NonEuclidean
Every tile in a hyperbolic tiling is randomly colored red or blue. How far should we move to find a specific pattern (a shape constructed out of tiles, with specific colors)?
The distance is usually proportional to \(n\), the number of tiles in the pattern -- this is because at a given location the pattern appears with probability \( 1/2^n \), and there are \(\Theta(c^d)\) possible locations in distance d.
So, for example, HyperRogue normally displays 582 tiles, and for every specific coloring of these 582 tiles, it should be somewhere in about 742 steps (and all of them in about 753 steps). If we used symbols (26 letters + space) instead of colors and were looking for a specific message of 1000 characters, it should appear in radius 6000.
Problem: however, it is not clear how to find such a pattern (and whether it would be still true for a given pseudorandom generator). What it the most elegant coloring algorithm with similar properties but where requested patterns can be found by following some procedure? (If you do not know how hyperbolic geometry works, might be easier to think about binary trees)
#NonEuclideanGeometry #NonEuclidean #HyperbolicGeometry #HyperRogue #roguelike #procgen
The largest Christmas decoration in a videogame!
#mathart #noneuclidean #NoneuclideanGeometry #roguelike #HyperRogue
We cannot tell how fast we are moving (for example, do not feel that Earth is moving very fast). This is related to how the objects move at constant speed in a straight line if no force is acting on them.
This is not the case in spherical or hyperbolic geometry, though (assuming a naive model of time*). In this visualization, every point in the yellowish "ghost" moves in a straight line at constant speed. The captain could tell how fast they are moving by measuring these distortions.
* not the case in (anti-)de Sitter spacetime, as in Relative Hell. https://zenorogue.itch.io/relative-hell
Added some enemy turrets to Relative Hell! (A game in anti-de Sitter spacetime)
These turrets are as accurate as they could possibly be -- they see our ship, and compute the shooting angle so that the ship would be hit if it did not accelerate in the meantime. This can be seen in the last part of the video where the ship does not accelerate.
Note "see" -- of course, the speed of light is limited in this game, so their information is rather outdated... The bullets move at speed close to the speed of light.
The visuals shown here are not what the player would see but rather a slice of the spacetime at t=0 relative to the ship (the turrets are deterministic so let us assume the ship's AI renders the current state). The "wobbling" of turrets seems to be caused by the Lorentz transformations as the spaceship accelerates.
Also new color scheme inspired by pop spacetime explanations, and using a different projection -- this is essentially Beltrami-Klein but it looks conformal because of the map's rotation causing length contraction. Less straightforward but looks better and less cells need to be rendered, which improves the performance.
RogueViz collection: https://store.steampowered.com/app/2271110/RogueViz_Collection/
And here is another conformal projection. (Obtained from the last one using inversion.)
A conformal mapping from ℍ²×𝕊¹ to 𝔼³. This is obtained by using the half-plane model for ℍ², let's say {(x,y): y>0}, and then adding the third dimension by rotating it in the 'yz' plane around the 'x' axis.
#NonEuclideanGeometry #NonEuclidean #RogueViz #mathart
Some improvements in Nil Rider before the Steam release of RogueViz [1]! Previously the game simply ended when you rode off the surface. Now, you can ride off to reach the layer below -- and because of how straight lines work in this geometry, you can drop directly below!
As explained in our video [2] without gravity objects follow helices, with radius smaller when the slope is closer to vertical. With gravity, the slope changes in time, so the projection of a freely falling unicycle is quite a funny curve (pink).
[1] https://store.steampowered.com/app/2271110/RogueViz_Collection/
[2] https://www.youtube.com/watch?v=FNX1rZotjjI
#RogueViz #nilrider #NonEuclidean #NonEuclideanGeometry #mathart #gamedev
Some social network analysis on Metroidvanias.
Data from https://www.reddit.com/r/metroidvania/comments/1dwqjp0/if_you_had_to_pick_5_of_the_best_metroidvanias/, two games are connected (with a weighted edge) when they appear in the same answer.
We arrange the games on the tiles, aiming to minimize the sum of (distance) * (weight). Hyperbolic geometry tends to be be good for this kind of visualization (closeness correlates to edge weight).
Tehora Rogue has run a community detection algorithm (using Gephi) on this network multiple times. This algorithm would find 4 to 6 communities in different runs, the 4 communities shown are based on aggregation of the results.
(There are "green" and "yellow" communities of sets of five games posted by "trolls" who have posted games not mentioned by anyone else, and the main genre splits into "blue" and "red" -- if you know these games, do you have any idea what the blue/red split could mean?
In the second picture, the red / blue / green components (excluding trolls) are determined by how often the game appeared in the same community as Iconoclasts / Cookie Cutter / Castlevania: Harmony of Despair. These three games were chosen because they frequently belonged to different communities.
#metroidvania #mathart #socialnetworkanalysis #gamedesign #rogueviz #NonEuclideanGeometry #NonEuclidean #tessellation
Our new video about the Thurston geometry we have not previously explained in our videos, "the universal cover of the 2x2 special linear group over reals". Why such a name? An exciting travel through spaces of motion, product, and twisted product geometries!
Nerds are so freaking cool.
5-Sided #Square - Numberphile
https://youtube.com/watch?v=n7GYYerlQWs&si=hjIW1K30XBLPsAV3