The essence of the general Lagrange multiplier method is looking for the common tangent or normal space between two high dimensional submanifolds or level sets associated with the objective function and multiple constraints.

https://jihuan-tian.github.io/math/2025/05/28/understanding-about-the-lagrange-multiplier-method.html

#differential_geometry #pde

Belle collaboration avec le Pôle Projets : Modélisation #Mathématique des Systèmes Complexes de #centralesupelec Université #parissaclay.
J'ai proposé un problème appliqué de modélisation par #PDE et de résolution numérique d'un processus de diffusion d'insectes avec piègeage, issu de mes travaux de recherche.
J'ai eu le plaisir d'accompagner le travail de Aya Chaieb, Baptiste Petiot, Louis Mudarra et de Lucas Bourret. Utile et enrichissant pour toutes les parties.
https://hal.inrae.fr/hal-05084285v1

New paper by #ModConFlex researcher Zhuo Xu on the robustness of a fluid-particle interaction system.

"A distinctive feature, not yet considered in the ISS literature, is that our system involves a free boundary. More precisely, the fluid is described by the viscous Burgers equation, and the motion of the particle obeys Newton second law. ... The proof is based on the construction of a Lyapunov functional derived from a special test function."

https://arxiv.org/abs/2505.08393

#PDE

#MSCA
#HorizonEU

[Перевод] 79% научных публикаций об AI завышают результат

Применение AI в науке растет, но результаты его внедрения часто переоценены. Исследования показывают, что 79% публикаций, заявляющих о превосходстве AI, используют некорректные бенчмарки. Это искажает представление о реальном потенциале AI в научном прогрессе.

https://habr.com/ru/articles/911800/

#ии #наука #исследование #машинное+обучение #физика #pde #оптимизация #методология #хайп #deepmind

Amar no es mirarse el uno al otro; es mirar juntos en la misma dirección.
.
.
.
.
.
(Antoine de Saint-Exupéry)
Palabras de Escritores.
31.2025, Argentina.
Abrazos | #PDE | #palabras #escritores #parejas #couples #literaverso #mastodon #fediverse

There are two kinds of projections when we solve a linear problem, either finite dimensional or infinite dimensional, which are used for solution representation and error measurement. They are important in the Petrov-Galerkin method.

#linear_algebra #pde

https://jihuan-tian.github.io/math/2025/05/20/two-kinds-of-projections-in-solving-linear-problems.html

I'm wondering: #physics makes a lot of use of #periodic functions, in particular it is very useful to solve space-dependent equations in representative volumes with #periodicBoundaryConditions.

However I've only seen it done with periodicity along orthogonal directions, aligned with a Cartesian frame.

Do you know of work, e.g. #PDE resolution, in nonrectangular #periodicDomains? E.g., in a #tiled hexagon? (but with a sufficiently generic setting, not exploiting regular hexagon symmetries) Even better if the periodicity parameters themselves are among the unknowns.

(Maybe I'm completely missing something obvious there, I'm in my first steps towards defining what I want - any random thought on the topic highly welcome!)

#tiling people?

I have arrived, and given my talk, at the tri-section #MAA meeting
#PDE #MathConference

Can anyone recommend a writeup on 1st order linear PDEs which is not written for engineering majors, but for working mathematicians? #PDE #math

#AI #MachineLearning #Safety #DiffusionModels #PDE #ConformalPrediction #TrustworthyAI

So I found https://github.com/tracel-ai/cubecl which allows #gpgpu in #rust. Already using it to calculate some determinants for triangulations. Wondering if it can be leveraged to build a numeric #pde solver

Effects of OpenCL-Based Parallelization Methods on Explicit Numerical Methods to Solve the Heat Equation

#OpenCL #PDE #Performance #Physics

https://hgpu.org/?p=29451

O planejamento urbano municipal enfrenta onda de empreendimentos verticais do tipo studio, que prometem aumentar a capacidade habitacional da cidade de São Paulo.

Embora eles instiguem o adensamento populacional nas regiões dotadas de infraestrutura, a nova gestão municipal segue com o desafio de rever o modelo de urbanismo corporativo e de priorizar as demandas coletivas. #Eleições #Urbanismo #GestãoPública #PDE

Leia o press release dos Estudos Avançados!

https://humanas.blog.scielo.org/blog/2024/09/19/enfoque-cooperativo-para-menos-studios-e-mais-igualdade-na-gestao-do-espaco-de-sao-paulo/

Wir freuen uns bei der diesjährigen Zyklenvorstellung insbesondere auf folgende Vortragende und Vorträge:

- Prof. Dr. Russell Luke, Variational #Analysis and #Optimization
- Prof. Dr. Ingo Witt, Analysis of partial differential equations (#PDE)
- Prof. Dr. Anja Sturm, Stochastische Prozesse
- Prof. Dr. Axel Munk, Statistical Foundations of #DataScience

My slides from the workshop at the Huawei Cyber Security Week https://www.fukami.eu/d/ossf-huawei-hcstcbxl-620.pdf

#PDE #CRA #NIS2 #CSAF #SBOM

Surprisingly many nonlinear partial differential equations of real interest have closed-form solutions: https://johndcook.com/blog/2024/04/25/closed-form-pde/

#physics #mathematics #PDE

Just found this little helper for #neovim, #lazyvim that lets you manage your node dependencies from within your editor.
I have already seen this in VSCode but never missed it until I installed it in my #pde

https://github.com/vuki656/package-info.nvim

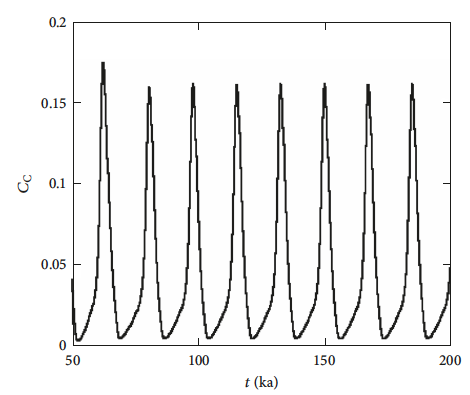
We've been working on a massive riddle tying together #self-organization, #carbonate #diagenesis, reactive transport, #paleoclimate and #Milankovich cycles, and very stiff PDE systems.

If you've missed the poster at #egu24, you can still find it attached to the abstract in the conference program (https://meetingorganizer.copernicus.org/EGU24/EGU24-16400.html) and on Zenodo https://zenodo.org/records/10943274 If you're into numerical methods, tricky PDEs or other aspects of #modeling, please see if you have any advice to us 😄 #solvers #PDE

Using AI libraries for Incompressible Computational Fluid Dynamics

#CFD #AI #FluidDynamics #PDE

https://hgpu.org/?p=29132

LINEAR TRANSPORT EQUATION
The linear transport equation (LTE) models the variation of the concentration of a substance flowing at constant speed and direction. It's one of the simplest partial differential equations (PDEs) and one of the few that admits an analytic solution.

Given \(\mathbf{c}\in\mathbb{R}^n\) and \(g:\mathbb{R}^n\to\mathbb{R}\), the following Cauchy problem models a substance flowing at constant speed in the direction \(\mathbf{c}\).
\[\begin{cases}
u_t+\mathbf{c}\cdot\nabla u=0,\ \mathbf{x}\in\mathbb{R}^n,\ t\in\mathbb{R}\\
u(\mathbf{x},0)=g(\mathbf{x}),\ \mathbf{x}\in\mathbb{R}^n
\end{cases}\]
If \(g\) is continuously differentiable, then \(\exists u:\mathbb{R}^n\times\mathbb{R}\to\mathbb{R}\) solution of the Cauchy problem, and it is given by
\[u(\mathbf{x},t)=g(\mathbf{x}-\mathbf{c}t)\]

#LinearTransportEquation #LinearTransport #Cauchy #CauchyProblem #PDE #PDEs #CauchyModel #Math #Maths #Mathematics #Linear #LinearPDE #TransportEquation #DifferentialEquations