Lmst

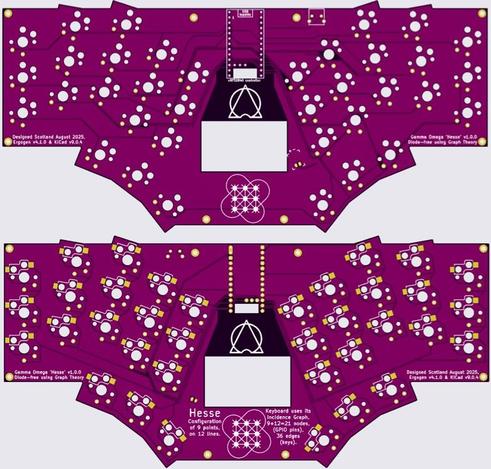
My second #ErgoMechKeyboard was also featured on this Keyboard news blog https://kbd.news/Gamma-Omega-Hesse-2762.html - as was my first https://kbd.news/Gamma-Omega-TC36k-2690.html and the prior #GraphTheory diode-less #MechanicalKeyboard designs like https://kbd.news/JESK56-2322.html and https://kbd.news/reJESK-2485.html

I'm serious. The best way to do computing is just over a nice cup of tea 🫖👵🏻

We're going to encode this into the graph as a pattern, it's the core protocol after all 🧸

#ai #platformengineering #graphtheory #justanicechatoveracupoftea

I am slowly getting better at soldering, 4 out of 7 successful #MechanicalKeyboard PCBs now - all three of my diode-free #GraphTheory wired keyboard PCB designs have worked (eventually) ⌨️🎊

1️⃣ #RaspberryPiPico #RP2040 ‘Gamma Omega TC36K’ (USB only) http://astrobeano.blogspot.com/2025/08/my-first-self-built-computer-keyboard.html

2️⃣ #ProMicro #nRF52840 BLE ‘Gamma Omega Hesse’ https://astrobeano.blogspot.com/2025/10/hesse-diode-free-bluetooth-keyboard.html

3️⃣ #SeeedStudio #Xiao #SplitKeyboard BLE split Forager ‘Acid’ http://astrobeano.blogspot.com/2025/10/partial-heawood-forager-keyboard.html

#ErgoMechKeyboard #ErgonomicKeyboard

Underside of the left hand’s half of the ‘Forager Acid’ split keyboard, with a transparent bottom case letting you see the blue PCB, LiPo battery (bottom middle), hot swap switch sockets, and Seeed Xiao controller (top right).

Today's reading: https://arxiv.org/abs/2509.16135v1
a brand-new paper on enumeration of perfect bipartite matchings.

Here's my theory:
1. For each solution (oval) remove it and its square neighbors from the graph G.
2. Compute the perfect matchings on the remaining graph G \ S. These are 1:1 with vertex covers, by Konig's theorem.

This gives us all minimum-number-of-clue puzzles with the given solution. Now we want any "worse" puzzles that do not have those as a subset.

3. For each square, treat it as part of the clue, but remove it from the graph to get G'', whose solution will be inefficient because it lacks that information.
4. Compute perfect matchings again, discarding any puzzles whose subsets are already known to be solvable puzzles.

That gives us minimum-plus-1; do we just have to repeat until we stop getting new solutions? Or can we solve some other problem to tell us when to stop? I don't love iterating over increasingly large subsets of "inefficient" clues.

So I'm trying to determine if the algorithm in the paper above can be adapted to produce less-than-perfect matchings.

#GraphTheory

Got to share my favorite “accidental poetry from a technical document” in my guest lecture today on graphs 🤓 #GraphTheory #ComputerScience #NetworkScience

A slide titled “special graphs” states: “A lobster is a tree that reduces to a caterpillar when pruning all leaf nodes. A caterpillar is a tree that reduces to a path graph when pruning all leaf nodes.”
From the Python NetworkX package dcocumentation

I’m excited to share that our article has been published: “Brain Topology Disruption in Early-Onset Dementia: Review of Current Findings and the Need for Network Resilience-Focused Models” (http://dx.doi.org/10.1002/brb3.70903)

In this review, we highlight several important insights:

- A summary of how early‐onset forms of dementia (including Alzheimer’s disease, frontotemporal dementia (FTD), and behavioral variant FTD) show disruption in brain network topology (both structural and functional) rather than purely focal pathology.

- Evidence that brain networks lose their optimal organisational properties (e.g., balance of segregation and integration) in early‐onset dementia, reflecting decline in network resilience. For example, previous work has shown disrupted segregation/integration in large‐scale brain networks in Alzheimer’s/MCI.

- The concept of network resilience as a key lens: rather than only asking “where damage occurs”, the paper argues we should ask “how the network topology fails to compensate, reorganise or maintain function under pathology”. This shifts the view to resilience‐focused models.

- Review of methodological findings: how graph‐theoretic metrics (clustering coefficient, global/local efficiency, modularity, assortativity, small‐worldness) are being applied to neuroimaging and electrophysiology in early dementia.

- Gaps and opportunities: the need for models that integrate network resilience, longitudinal data, multimodal connectivity (structural + functional + electrophysiological) and early‐onset cohorts; and the translational potential for biomarkers and interventions that support network integrity rather than just reduce pathology.

I believe this work contributes to bridging neuroscience, network theory, and clinical neurology, and invites discussion on how we can design interventions that strengthen brain network resilience in dementia.

Thanks to my co-authors (Hema Nawani, Sredha Sunil) and reviewers, and a huge thank you to our professor Veeky Baths for his guidance and support throughout this work.

If you’re working in cognitive neuroscience, network approaches to brain disorders, early‐onset dementia, connectomics or translational neurology, let’s collaborate to make a real impact.

#Neuroscience #BrainNetworks #Dementia #EarlyOnsetDementia #Neurodegeneration #NetworkResilience #ClinicalNeuroscience #GraphTheory #NetworkNeuroscience #ComputationalNeuroscience

Several of my #PurdueFortWayne #Math colleagues retired shortly after the 2020 pandemic outset, and some since then, and we finally had a retirement dinner celebration for all of them. (particularly famous among them, graph theorist L. Beineke :k33: :k5: )

Lots of photos:
https://photos.app.goo.gl/mz78CL8aewmtRK759
#GraphTheory #HistoryOfMath

And then there were two: This post was typed on my phone using my first self built Bluetooth #ErgoMechKeyboard, running on battery power with #ZMK firmware: the Gamma Omega Hesse. Like my other #MechanicalKeyboard designs this has a diode-free PCB using #GraphTheory. https://github.com/unspecworks/gamma-omega/tree/main/hesse

Small 36-key mechanical keyboard in a black resin 3D printed case with Chosfox CFX square keycaps in black (home row and thumb keys), orange (top and bottom on left), and robin blue (top and bottom on right). The middle thumbs have a 1.25u keycap, as do the S&L keys (could do this at D&K instead), which fit because these are slightly smaller than the Kailh Choc keycaps this case was designed for. The index and pinky home keys have a homing bumb.

Two small black keyboards, on the left with a USB cable the wired only Gamma Omega TC36K (with purple MKB keycaps), and on the right showing a reset button and USB port on the top edge, the wireless Gamma Omega Hesse (with blue, black, and orange CFX keycaps).

Here's a blatantly false statement:

Let G be a cubic #graph embedded in the plane with a proper 3-edge colouring. Colour a vertex black if the clockwise ordering of the colours of its incident edges is rgb and white if the ordering is rbg. Then the number of black vertices is equal to the number of white vertices.

I asked #chatgpt to **prove or find a counterexample** to the above statement.

It confidently gave a wrong proof. It persisted even when I gave counterexamples to its intermediate steps.

When I asked (in a new chat) to find the smallest counterexample to the claim it was immediately able to do so!

It's hard to be sure of the model; I think it's 5.1. But I think there's something to learn from here.

#llm #graphTheory

Gave a lecture today about Euler's theorem.
Then somehow it led to:
"There's a face, next muffin!"
Wondering what kind of vibe that sent out...

#teaching #graphtheory #euler

A new inquiry activity is posted on Fractal Kitty!

https://www.fractalkitty.com/inquiries-week-5-triangles-emerge/

This one plays with graphs and can be used as an extension to Sim, Don't Make a Triangle, and other such games.

#mtbos #iteachmath #mathplay #accessibleProofs #inquiry #turan #graphTheory #triangles

doing some things trying to reproduce an #OEIS sequence

I get matching numbers for n = 0,1,2,3,4,5 but my result for n=6 is off by one (I miss one item).

Naturally the example given is for n=5, and no example for n=6.

I think my assumption is off, if two non-isomorphic hypergraphs can yield isomorphic incidence graphs? perhaps, seeing as a hypergraph's incident graph is bipartite, what if the roles of each part were reversed?

#maths #GraphTheory

After just shy of 14 years living here, I will begin tomorrow to give (math) lectures in Dutch.

#teaching #dutch #graphtheory

Two properties of a mathematical graph, mentioned in consecutive exercises in Sedgewick & Wayne's algorithms textbook, are "girth" and "Wiener index".

#mathematics #GraphTheory #algorithms

Here's some new work that came from last month's Sparse (Graphs) Coalition session on Ramsey numbers:

https://mathstodon.xyz/@WouterCvB/115418077892309375

#combinatorics #ExtremalCombinatorics #graphtheory #remoteconferences

📘 New preprint
“Semantic Analysis in the Context of Jewish Theology and the Symbolism of the Kabbalistic Treatise Sefer Yetzirah”
DOI: https://doi.org/10.5281/zenodo.17378184

This study develops a formal methodology for semantic analysis based on the symbolic system of Sefer Yetzirah — interpreting the sefirot and Hebrew letters as a conceptual network.

#DigitalHumanities
#ComputationalHermeneutics #Kabbalah #JewishStudies #SemanticAnalysis #Judaism #GraphTheory #linguistics

New paper on arxiv:

https://arxiv.org/abs/2510.15553

Linda Cook, Eileen Robinson, Gabriëlle Zwaneveld and I used the claw-free structure theorems to prove an important special case of a conjecture of Vu.

#combinatorics #graphtheory #arxiv

#Mathober #Mathober2025

The prompt for day 5 was 'Digraph Sink'. In mathematics 'digraph' is an abbreviation for 'directed graph' which is a kind of network made by joining nodes with arrows. A 'digraph sink' is any node which has no arrows that point out of it. If you walk around a digraph by following the arrows then the sinks are the places where you can get stuck.

In linguistics a 'digraph' is instead a pair of letters that make a different sound when written together than you would expect from their individual sounds. Let's draw a digraph digraph where the nodes are the letters of the alphabet, and the arrows represent which pairs of letters form digraphs.

The sinks in this digraph are B, D, F, H, J, K, L, M, V, X, Y and Z.

#Math #Maths #Mathematics #GraphTheory #Linguistics #Orthography #EnglishOrthography

A network with 26 points labled by letters, and arrows joining some of the points. The letters BDFJLMVXY are isolated points off to one side, while the rest are all connected. The letters H and I have the most arrows in to them, and E and O have arrows to themselves.

The #Mathober Day 9 prompt is ‘Chi’. In graph theory, \(\chi(G)\) denotes the chromatic number of a graph \(G\): the minimum number of colours required to colour all vertices so that no adjacent vertices have the same colour.

The famous ‘four colour theorem’ says that all planar graphs \(G\) have \(\chi(G) \leq 4\). A graph is planar if it can be drawn in the plane without any edges crossing.

The conjecture originated in 1852 when Francis Guthrie (1831–99) noticed that it was possible to colour a map of England using only four colours so that no neighbouring counties received the same colour, and wondered if this held true for all maps. The question for maps is transformed into one for graphs by replacing each region by a vertex and placing edges between vertices corresponding to neighbouring regions.

Thus, for the Mathober prompt ‘Chi’, I offer a map of the counties of England as they were in Guthrie's time and the corresponding graph, coloured in the same way with four colours.

Vector version (PDF format) of the map: https://ajcain.codeberg.page/posts/files/england-counties-map-4coloured.pdf

Vector version (PDF format) of the graph: https://ajcain.codeberg.page/posts/files/england-counties-graph-4coloured.pdf

1/2

#Mathober2025 #GraphTheory #HistMath