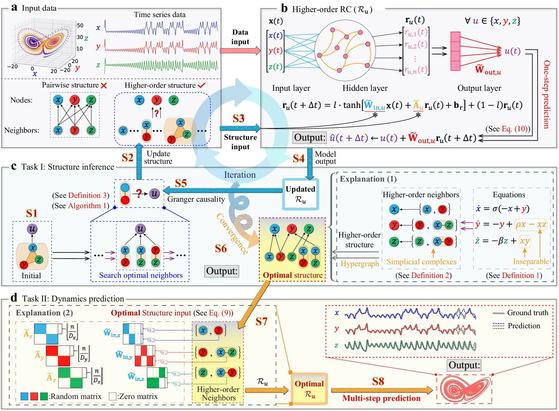
#simplicialcomplex + #Causality +#Reservoircomputing:
"Higher-order Granger reservoir computing: simultaneously achieving scalable complex structures inference and accurate dynamics prediction" https://www.nature.com/articles/s41467-024-46852-1

#dynamicalsystem #ML #AI

Saddles and stable nodes in a nonlinear #DynamicalSystem. From example 6.3.1 in Steven Strogatz's textbook on #NonlinearDynamics and #Chaos. Simulated with #BrainDynamicsToolbox.

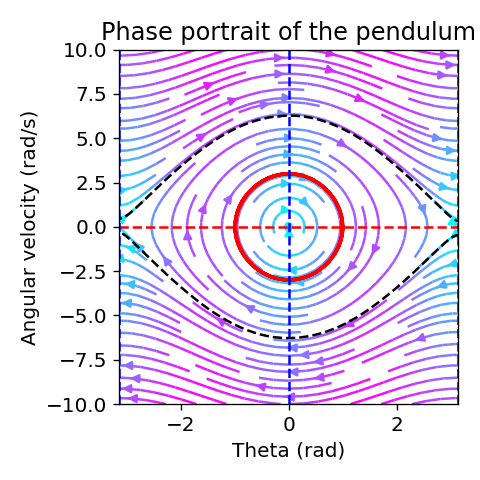
The damped and driven #pendulum is a classic #nonlinear #DynamicalSystem in physics. Simulated here with the #BrainDynamicsToolbox.

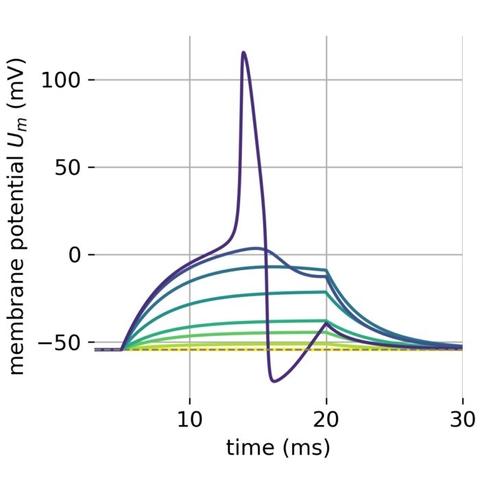
An important step in #ComputationalNeuroscience 🧠💻 was the development of the #HodgkinHuxley model, for which Hodgkin and Huxley received the #NobelPrize in 1963. The model describes the dynamics of the #MembranePotential of a #neuron 🔬 by incorporating biophysiological properties. See here how it is derived, along with a simple implementation in #Python:

🌍 https://www.fabriziomusacchio.com/blog/2024-04-21-hodgkin_huxley_model/

Feel free to share and to experiment with the code.

#CompNeuro #PythonTutorial #NeuralDynamics #DynamicalSystem

Here is another #PhasePlaneAnalysis #tutorial, this time applied to the #VanDerPolOscillator, a non-conservative #oscillator with nonlinear damping:

🌍 https://www.fabriziomusacchio.com/blog/2024-03-24-van_der_pol_oscillator/

#DynamicalSystem #ComputationalScience #PhasePortraits #Python

Exploring the behavior of #DynamicalSystems directly through their differential equations can be complex. #PhasePlaneAnalysis offers a clearer and intuitive view by visualizing dynamics with #PhasePortraits, simplifying understanding. Here is a #tutorial along with some #Python code, exploring this method and exemplarily applying it to the simple pendulum.

🌍 https://www.fabriziomusacchio.com/blog/2024-03-17-phase_plane_analysis/

#ChaoticSystems #DynamicalSystem #ComputationalScience

Genuary Prompt Nr. 5 is "In the style of Vera Molnàr". When I looked at her works I liked the framing squares with things going on in them. They reminded me at what I saw when investigating Dynamical Systems. This is 8 iterations of the function f(x,y)=( x-(1+y/4)tan(y)-t*y , x )

Full-Res full-length full-size version: https://youtu.be/q8V0KPQRjRM

#genuary #genuary5 #genuary2024 #dynamicalsystem

Mapping the complex plane.
Using an image of a flower for coloring.

https://gitlab.com/metagrowing/ana/-/blob/master/visual_server/media/frag/cmplx/cmplx-03.frag

https://gitlab.com/metagrowing/ana/-/blob/master/live_coding/src/demo/cmplx/cmplx-03.clj

#dynamicalsystem #openFrameworks

@noneuclideandreamer Again, this iterative mapping in the complex plane. This time with adjustable color spectrum and denoised.

for(int l=0; l<9; ++l) {
_xy = vec2(_xy.y + sin(t * _xy.x),
_xy.x);
}

#dynamicalsystem

Soapy Function:

(x,y)=(y+tlog|x|,x)

(better resolution on youtube)

#mastoart #codeart #dynamicalsystem

Proudly presenting this month's High-res Render for Patrons of Level Square and up: full size 25600×25600 pixels

If you try to "magic eye" it, it shimmers!

It's my favorite of the iteration functions I explored: (x,y)=(x-t*tan(y),x).
The squares have a side length of pi, due to tan of course.
Squares below each other would actually look the same since it does only depend on y%pi via tan. So I discretely jumped my t-value from 1.1 over 1 to 0.9.

#mathart #codeart #fractal #blackandwhite #dynamicalsystem #mastoart

This palette took me by surprise. 😅

Movie not compressable to masto size, so stills it is!

#mastoart #codeart #dynamicalsystem #attractor #fractal (mostly) #blackandwhite

Bogdanov Map, I am so glad I found you!

#mastoArt #codeArt #dynamicalsystem #attractor #bogdanov

@karlo

The #state I’m talking about is the present state of every living #DynamicalSystem which is controlled by the closed autopoietic process of #growth and #learning:

#Meaning is usually described with #VectorSpace #Semantics as in the article below comparing the works from #CAShannon and #AMTuring:

https://www.journals.uchicago.edu/doi/full/10.1093/bjps/axx029

Basically, what vector space semantics says is that the meaning of a message depends on the #Context provided by the sender’s and the receiver’s #DynamicalSystem #Knowledge #State.

As they are two different physical entities they will obviously be in different states, so the two meaning can never be exactly the same.

For modelling non-linear dynamical systems on a mesh, you can "lift" the states using some function such that you have a linear operation in a higher dimensional space. Koopman operators are the linear operators in Hilbert spaces, and recently neural networks have been applied to learn system dynamics in this space. This paper proposes a pytorch module for Koopman Neural Operators.

#MachineLearning #DynamicalSystem #NeuralOperators
https://arxiv.org/abs/2301.01104

@systemspractitioner

I understand many people are comfortable with VSM but I never used it and I find it cumbersome and complicated to understand. I worked with companies using #CMMI, #ISO, #6Sigma, #SCRUM, along with a few other standards and frameworks and, apart from my #DynamicalSystem model, which I use to explain practically everything these days 😀, I try not to have strong preferences for specific tools and frameworks and try to learn first how what the company is currently using and familiar with can be re-used, tweaked or augmented to achieve their goals for the future.

@bbak @kironbondale @joeposaurus

Where did you get the idea that I equate policies and culture?

Stories songs, and other documents are never just a description of the culture that created them. As you correctly identified, when they are accepted by the masses as a #Standard, they can be a powerful means for culture specific motivation and control (constraint).

In the end, it really does not matter if your organization is a #Kanban, a #Scrum, or some other #Culture. Every (people) organization is a #DynamicalSystem with #Memory.

#arxivfeed :

"A Novel Hypothesis for Migraine Disease Mechanism: The Creation of a New Attractor Responsible for Migraine Disease Symptoms"
https://www.biorxiv.org/content/10.1101/2022.11.13.516319v1

#ComputationalNeuroscience #neuroscience #neuro #neuroimaging #EEG #DynamicalSystem #attractor #migraine