@mcnees
Valuable info to know how to calculate should you be locked in a school bus without technology and slowly invaded by huge Australian spiders
https://youtu.be/TLOKpJcIp98
#fractaldimension
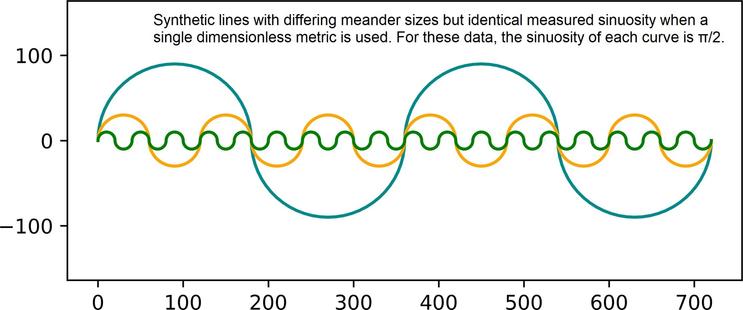
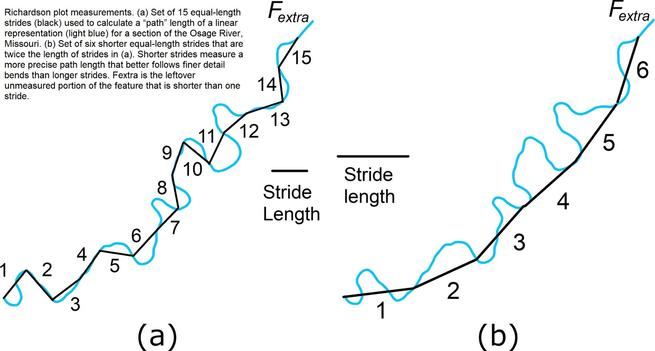
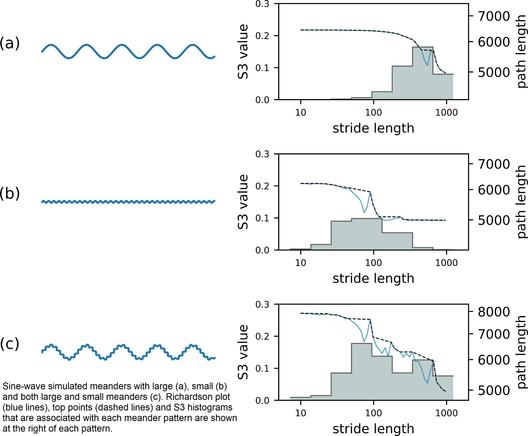
At What Scales Does A River Meander? Scale-Specific Sinuosity (S3) Metric For Quantifying Stream Meander Size Distribution
--
https://doi.org/10.1016/j.geomorph.2023.108734 <-- shared paper
--
“HIGHLIGHTS:
• Scale-specific sinuosity (S3) summarizes bend sizes of linear features and associated contributions to sinuosity across a range of scales.
• The S3 plot is analogous to a frequency histogram of bend sizes, like a fingerprint or a spectral signature
• The S3 is an easily computed metric to assess influential scales in bend patterns of linear stream features
• The paper formalizes a relation between sinuosity and fractal dimension..."
#GIS #spatial #mapping #multiscale #water #hydrography #streamgeometry #meanderpattern #meander #fractaldimension #sinuosity #model #modeling #spatialanalysis #bends #distribution #S3 #fractals #geometry #landscape #geomorphology #geomorphometry #prediction #spatialanalysis #coast #coastal #automatedanalysis #riverbend #appliedscience
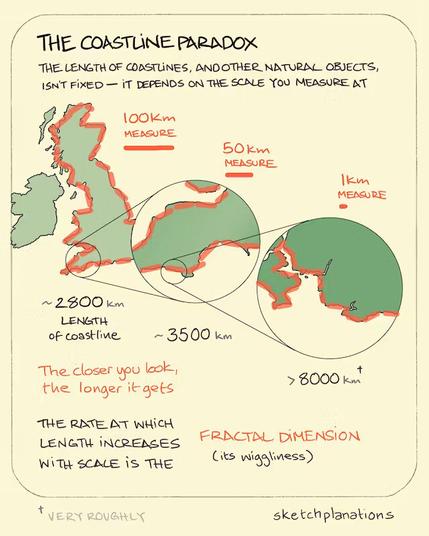
The Coastline Paradox [measurement]
--
https://sketchplanations.com/the-coastline-paradox <-- shared technical article 1
--
https://ars.electronica.art/keplersgardens/en/coastline-paradox/ <-- shared technical article 2
--
#GIS #spatial #mapping #gischat #coastlineparadox #coastline #measurement #metric #scale #scaledependency #fractal #research #math #mathematics #Mandelbrot #wiggliness #accuracy #precision #map #cartography #relative #length #generalisation #fractaldimension #fractal #rivers #borders #appliedscience
The intricacy of the #fjords not only makes for a majestic landscape but increases the coastline geometric complexity, which can be quantified using #FractalDimension...
We are used to 1, 2 and 3 dimensions, for examples lines, squares and cubes, respectively, and we intuitively understand that complexity increases with increasing dimensions...