Analytic Hyperbolic Geometry: Mathematical Foundations and Applications by Abraham Albert Ungar (PDF)
Author: Abraham Albert Ungar
File Type: PDF
Download at https://sci-books.com/analytic-hyperbolic-geometry-mathematical-foundations-and-applications-9812564578/
#Analytic, #AbrahamAlbertUngar

Why is Ukraine losing its technological advantage in the drone war, and how can an effective management system be established?
This topic is discussed in the article Why Are We Losing the Drone War — And What Can Be Done About It? by Yurii Kasianov, an officer in the Ukrainian Armed Forces, radio engineer and aerial reconnaissance specialist.
#warinukraine #analytic #ZNUA
https://zn.ua/eng/why-are-we-losing-the-drone-war-and-what-can-be-done-about-it.html

Contributions to Automorphic Forms, Geometry, and Number Theory: A Volume in Honor of Joseph Shalika 1st Edition by Haruzo Hida (PDF)
Author: Haruzo Hida
File Type: PDF
Download at https://sci-books.com/contributions-to-automorphic-forms-geometry-and-number-theory-a-volume-in-honor-of-joseph-shalika-1st-edition-0801878608/
#Analytic, #HaruzoHida

Recent Trends in Lorentzian Geometry (Springer Proceedings in Mathematics & Statistics Book 26) 2013th Edition by Miguel Sà¡nchez (PDF)
Author: Miguel Sánchez
File Type: PDF
Download at https://sci-books.com/recent-trends-in-lorentzian-geometry-springer-proceedings-in-mathematics-statistics-book-26-2013th-edition-b00akifkt8/
#Analytic, #MiguelSánchez

We are now concerned with more radical possibilities.

A paradigmatic example is topology.

In modern “analytic topology”, a “space” is defined to be a set of points equipped with a collection of subsets called open,
which describe how the points vary continuously into each other.
(Most analytic topologists, being unaware of synthetic topology, would call their subject simply “topology.”)

By contrast, in synthetic topology we postulate instead an axiomatic theory, on the same ontological level as ZFC,
whose basic objects are spaces rather than sets.

Of course, by saying that the basic objects “are” spaces we do not mean that they are sets equipped with open subsets.

Instead we mean that “space” is an undefined word,
and the rules of the theory cause these “spaces” to behave more or less like we expect spaces to behave.

In particular, synthetic spaces have open subsets (or, more accurately, open subspaces),
but they are not defined by specifying a set together with a collection of open subsets.

It turns out that synthetic topology, like synthetic set theory (ZFC), is rich enough to encode all of mathematics.

There is one trivial sense in which this is true:
among all analytic spaces we find the subclass of indiscrete ones,
in which the only open subsets are the empty set and the whole space.

A notion of “indiscrete space” can also be defined in synthetic topology,
and the collection of such spaces forms a universe of ETCS-like sets
(we’ll come back to these in later installments).

Thus we could use them to encode mathematics, entirely ignoring the rest of the synthetic theory of spaces.
(The same could be said about the discrete spaces,
in which every subset is open;
but these are harder (though not impossible) to define and work with synthetically.

The relation between the discrete and indiscrete spaces,
and how they sit inside the synthetic theory of spaces,
is central to the synthetic theory of cohesion,
which I believe David is going to mention in his chapter about the philosophy of geometry.)

However, a less boring approach is to construct the objects of mathematics directly as spaces.

How does this work?
It turns out that the basic constructions on sets that we use to build (say) the set of real numbers have close analogues that act on spaces.

Thus, in synthetic topology we can use these constructions to build the space of real numbers directly.

If our system of synthetic topology is set up well,
then the resulting space will behave like the analytic space of real numbers
(the one that is defined by first constructing the mere set of real numbers and then equipping it with the unions of open intervals as its topology).

The next question is,
why would we want to do mathematics this way?

There are a lot of reasons,
but right now I believe they can be classified into three sorts:
modularity,
philosophy, and
pragmatism.

(If you can think of other reasons that I’m forgetting, please mention them in the comments!)

By “#modularity” I mean the same thing as does a programmer:

even if we believe that spaces are ultimately built analytically out of sets,
it is often useful to isolate their fundamental properties and work with those abstractly.

One advantage of this is #generality.
For instance, any theorem proven in Euclid’s “neutral geometry”
(i.e. without using the parallel postulate)
is true not only in the model of ordered pairs of real numbers,
but also in the various non-Euclidean geometries.

Similarly, a theorem proven in synthetic topology may be true not only about ordinary topological spaces,
but also about other variant theories such as topological sheaves, smooth spaces, etc.

As always in mathematics, if we state only the assumptions we need, our theorems become more general.

#analytic #synthetic

Mike Shulman:

Mathematical theories can be classified as analytic or synthetic.

An #analytic theory is one that analyzes, or breaks down, its objects of study, revealing them as put together out of simpler things,
just as complex molecules are put together out of protons, neutrons, and electrons.

For example, analytic geometry analyzes the plane geometry of points, lines, etc. in terms of real numbers:
points are ordered pairs of real numbers, lines are sets of points, etc.

Mathematically, the basic objects of an analytic theory are defined in terms of those of some other theory.

By contrast, a #synthetic theory is one that synthesizes,
or puts together,
a conception of its basic objects based on their expected relationships and behavior.

For example, synthetic geometry is more like the geometry of Euclid:
points and lines are essentially undefined terms,
given meaning by the axioms that specify what we can do with them
(e.g. two points determine a unique line).

(Although Euclid himself attempted to define “point” and “line”,
modern mathematicians generally consider this a mistake,
and regard Euclid’s “definitions”
(like “a point is that which has no part”)
as fairly meaningless.)

Mathematically, a synthetic theory is a formal system governed by rules or axioms.

Synthetic mathematics can be regarded as analogous to foundational physics,
where a concept like the electromagnetic field is not “put together” out of anything simpler:
it just is, and behaves in a certain way.

The distinction between analytic and synthetic dates back at least to Hilbert,
who used the words “genetic” and “axiomatic” respectively.

At one level, we can say that modern mathematics is characterized by a rich interplay between analytic and synthetic
— although most mathematicians would speak instead of definitions and examples.

For instance, a modern geometer might define “a geometry” to satisfy Euclid’s axioms,
and then work synthetically with those axioms;
but she would also construct examples of such “geometries” analytically,
such as with ordered pairs of real numbers.

This approach was pioneered by Hilbert himself, who emphasized in particular that constructing an analytic example (or model) proves the consistency of the synthetic theory.

However, at a deeper level, almost all of modern mathematics is analytic, because it is all analyzed into set theory. Our modern geometer would not actually state her axioms the way that Euclid did; she would instead define a geometry to be a set
P of points together with a set
L of lines
and a subset of
P×L representing the “incidence” relation, etc.

From this perspective, the only truly undefined term in mathematics is “set”, and the only truly synthetic theory is Zermelo–Fraenkel set theory (ZFC).

This use of set theory as the common foundation for mathematics is, of course, of 20th century vintage,
and overall it has been a tremendous step forwards.

Practically, it provides a common language and a powerful basic toolset for all mathematicians.

Foundationally, it ensures that all of mathematics is consistent relative to set theory.

(Hilbert’s dream of an absolute consistency proof is generally considered to have been demolished by Gödel’s incompleteness theorem.)

And philosophically, it supplies a consistent ontology for mathematics, and a context in which to ask metamathematical questions.

However, ZFC is not the only theory that can be used in this way.
While not every synthetic theory is rich enough to allow all of mathematics to be encoded in it,
set theory is by no means unique in possessing such richness.

One possible variation is to use a different sort of set theory like ETCS,
in which the elements of a set are “featureless points” that are merely distinguished from each other,
rather than labeled individually by the elaborate hierarchical membership structures of ZFC.

Either sort of “set” suffices just as well for foundational purposes, and moreover each can be interpreted into the other.
https://golem.ph.utexas.edu/category/2015/02/introduction_to_synthetic_math.html

Starting the next set of episodes in the Sadler's Lectures podcast, here's the first one on John Wisdom's excellent analytic philosophy of religion piece, "Gods", this one looking at differences between theists and atheists

https://soundcloud.com/gregorybsadler/john-wisdom-gods-differences-between-theists-and-atheists
#Podcast #Philosophy #Wisdom #Religion #Analytic #Atheists #Theists

GROW YOUR BUSINESS IN DIGITAL WORLD BY DIGTAL MARKETING STARTEGY#NIDMINDIA #SEO #ANALYTIC
https://nidmindia.com/

Attend the IEEE webinar "Artificial intelligence #AI for energy systems".
📅 31/05/2024
⌛ 10:00 - 13:00 (CET)
OMEGA-X partner UPC is hosting this webinar and deepdives in the #data #analytic services deployed within the OMEGA-X project.

https://events.vtools.ieee.org/m/421203

Whenever I walk to/from home, I have to walk up/down an inclined street; I noticed that the asphalt floor has different curvatures depending on how near it is of a bend, and I try to find a less steep incline while walking.

This got me inspiration for the few questions below. Any simple explanations, and related links, are welcome.

Given a #differentiable surface within R^3, and two distinct points in it, there are infinitely many differentiable paths from one point to another, remaining on the surface. At each point of the #path, one can find the path's local #curvature. Then:

- Find a path that minimizes the supreme of the curvature. In other words, find the "flattest" path.

- Find a path that minimizes the variation of the curvature. In other words, find a path that "most resembles" a circle arc.

Are these tasks always possible within the given conditions? Are any stronger conditions needed? Are there cases with an #analytic solution, or are they possible only with numerical approximations?

#Analysis #DifferentialGeometry #Calculus #DifferentialEquations #NumericalMethods

Mastering Google Analytics 4: The Best GA4 Courses in 2024

Looking for comprehensive training in Google Analytics 4? We've compiled the top paid and free GA4 courses available in 2024. Perfect for anyone keen to enhance their data analytics skills, these courses cover everything from the fundamentals of GA4 to its most advanced features. In this article, we've curated a list of the best GA4 courses and training programs for 2024.

https://www.linkedin.com/pulse/mastering-google-analytics-4-best-ga4-courses-analyzify

#google #ga4 #course #free #analytic

One of the distinctions central to Immanuel Kant's work is that between analytic and synthetic. Here's a core concept video looking at his discussion of that early on in the Prolegomena To Any Future Metaphysics

https://youtu.be/390JHuDsMUw
#Video #Kant #Distinction #Philosophy #Analytic #Synthetic #Metaphysics #Judgements

@katchwreck I agree that basic physical quantities can be defined through an integral, most notably the action integral leading to Laplace's equations. I also agree that an integral tends to smooth its integrand.

Have you considered that the integrands themselves are already smooth due to being analytic? The idea is that physics, at least classically, depends on analytic functions, which by definition are already the smoothest functions available.

There was a major effort in the early 60s to extend this idea to quantum field theory. It was called the analytic S-matrix program, and was the hottest thing in physics until quarks came along. The concepts behind the analytic S-matrix still appear from time to time when field theory gets too complicated to calculate. Given the "success" of string theory, who knows what the future holds for #analytic #functions in #physics.

Filosofian ja empiiristen tieteiden suhdetta pohtii kiintoisasti Catarina Dutilh Novaesin DN-essee synteettisestä filosofiasta,

https://dailynous.com/2023/05/30/a-plea-for-synthetic-philosophy-guest-post/

Filosofiassa 'synteettinen' ei merkitse keinotekoista tai ei-analyyttista, vaan empiirisesti tiedettävissä olevan integrointia käsitteelliseen tutkimukseen ja pyrkimystä hahmottaa "metsää" erityistieteiden "puilta".

#filosofia #philosophy #method #metodi #ethos #analyysi #analytic #synthetic #tiede #science

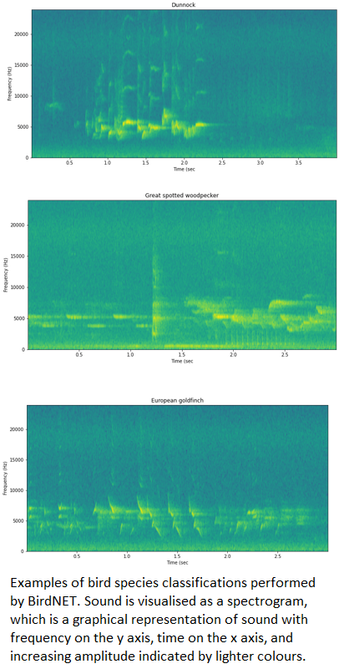
‘Only AI Made It Possible’ - Scientists Hail Breakthrough In Tracking British Wildlife [spatial analysis]
--
https://www.theguardian.com/technology/2023/aug/13/only-ai-made-it-possible-scientists-hail-breakthrough-in-tracking-british-wildlife <-- shared media article
--
#GIS #spatial #mapping #remotesensing #wildlife #cameratraps #audio #UK #England #Britain #bats #birds #mammals #railines #AI #artificialintelligence #cameras #spatialanalysis #spatiotemporal #monitoring #biodiversity #identification #analytic #ZSL #scale #rail #railindustry #transportation #infrastructure #tracking #animalbehavior #microphones #recording
#ZoologicalSocietyofLondon

Constance Jones solved Frege’s Puzzle (morning/evening star and the meaning of analytic statements) before Frege. Fantastic article about wrongly forgotten pioneering women in philosophy. #philosophy #analytic https://aeon.co/essays/the-lost-women-of-early-analytic-philosophy

If you want to keep a pulse on your business, #data #analytic systems are the mission-critical solution you need. Let me help you with connecting your systems to surface your key performance indicators with one-click. Providing you with insights and trends into how and where your money is being spent and what is producing #profitable returns.

150 (or so) Arguments for #Atheism

"A popular view in contemporary #analytic #philosophy of #religion is that while there are many arguments for #theism -- #cosmological, #ontological, and #teleological arguments; #moral arguments; arguments from #consciousness; etc. (...) -- there are only one or two arguments for atheism, viz., the problem of #evil and (more recently) the argument from #divine hiddenness.

This is a misconception. Here are well over 150"

http://exapologist.blogspot.com/2022/06/120-or-so-arguments-for-atheism.html

@philosophy