Lmst

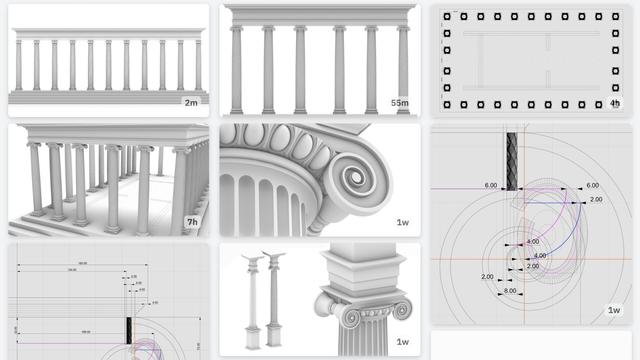
#Milestone9 - #ArcadeIntercolumniation #Keystone and #Modillion

#Arch without Pedestal https://pixelfed.social/p/Splines/803615973439041638

#Arch with #Pedestal and Keystone https://pixelfed.social/p/Splines/804537414363507454

#Keystone and #Dentil Details https://pixelfed.social/p/Splines/804548474524642209

#Modillion Details https://pixelfed.social/p/Splines/805587292338863257

#ModernEntablature with Detail https://pixelfed.social/p/Splines/805607059171193759

#Milestone8 - #SimpleIntercolumniation https://pixelfed.social/p/Splines/803106316515798367

#Milestone7 - Complete #IonicOrder https://pixelfed.social/p/Splines/800050647761776920

#Milestone6 — #Braids #3StrandBraids https://pixelfed.social/p/Splines/799602946527813102

#Milestone5 — #EggsAndDarts https://pixelfed.social/p/Splines/797069447808333887

#Milestone4 — #IonicScroll https://pixelfed.social/p/Splines/795361973789834465

#Milestone3 — #IonicColumn https://pixelfed.social/p/Splines/792803978865652429

#Milestone2 — Classic #IonicEntablature https://pixelfed.social/p/Splines/791021871062069787

#Milestone1 — #IonicPedestal https://pixelfed.social/p/Splines/790752092700055739

#Milestone7 - Complete #IonicOrder with fluted and unadorned #IonicColumn with details of #decorativeElements

#Milestone6 — #Braids #3StrandBraids https://pixelfed.social/p/Splines/799602946527813102

#Milestone5 — #EggsAndDarts https://pixelfed.social/p/Splines/797069447808333887

#Milestone4 — #IonicScroll https://pixelfed.social/p/Splines/795361973789834465

#Milestone3 — #IonicColumn https://pixelfed.social/p/Splines/792803978865652429

#Milestone2 — Classic #IonicEntablature https://pixelfed.social/p/Splines/791021871062069787

#Milestone1 — #IonicPedestal https://pixelfed.social/p/Splines/790752092700055739

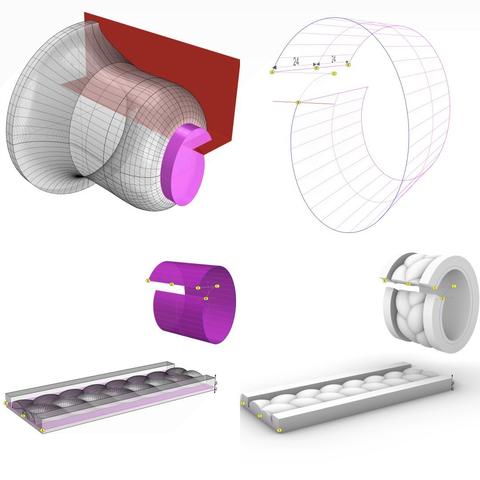
#3StrandBraids #FlowOnSurface

In the top-left, the highlighted magenta portion shows the interface between the #braids assembly and the #IonicScroll from https://pixelfed.social/p/Splines/795276076797088402.

Extract the #profileCurve shown as ABC in the top-right where the interface meets the scroll.

In https://pixelfed.social/p/Splines/794199123072358090, we rebuilt curves from 2nd-degree arcs to 3rd-degree NURBS for smoothness and swept the scroll surface one set of arcs at a time.

Now we have to flow braids on a single surface in one operation. So we need to combine the separate segments into a single NURBS curve. To do that, #explode the profile curve into individual segments, discard the straight portion, and join the curved portions.

Curves and surfaces have a #direction that you can change in the #CAD tool. Check that the direction of the joined curve is A to C, not C to A, and flip it if necessary. Then divide the curve at 120 units starting at A. This is marked by point B. Split the curve AC at B so that AB is 120 units long.

At this point AB is still made up of 5 segments, and exploding it would again decompose the curve into separate segments. So #rebuild AB as a single NURBS curve with 32 sections.

#Extrude AB to get a 48 units wide surface shown in magenta in the top-right. Point D is at the midpoint of AE and lies on the XZ plane.

Slice the channel assembly so that it is 8 units tall, 6 of which will be above the #tectonicSurface for the braid and 2 below. The tectonic surface is shown in the bottom-left as the flat magenta surface on the channel and the curved magenta surface for the scroll neck.

Flow the entire braid and channel assembly along the curved surface lining up points A, D, and E. For the vertical part on the side of the capital, just use the 33 unit tall block from https://pixelfed.social/p/Splines/799340150182400358 and bury 1 unit inside the #ovolo.

This concludes 3-strand braids. Only the non-essential #column #flutes remain.

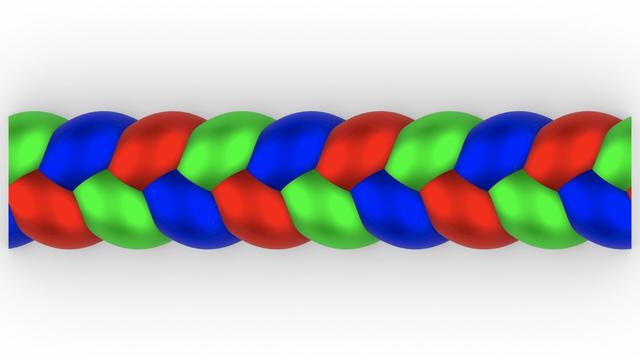
#3StrandBraids

#Braids are the last of the #decorative elements on the #IonicScroll, but like #EggsAndDarts, they are not specific to the #IonicOrder.

Braids are a popular design motif that find wide currency in modern #hairstyle, #fashion, and fashion accessories like #belts and #bracelets.

Braids come in infinite varieties with varying number of strands, thickness of strands, roundness or flatness of strands, and how tightly or loosely they are wound together. Here, I focus on the 3-strand variant mentioned in #Vignola's book and previewed in https://pixelfed.social/p/Splines/792015485979791089. The image here is brightly colored to draw attention to the 3 strands.

The geometry of braid strands is not at all obvious despite how familiar they look. Also, a braid strand is the only feature in the entire iconic order whose geometry cannot be captured with straight lines and circular arcs. Instead, a strand geometry must be defined in a series of steps starting with a basic #sinusoidal curve.

A sinusoidal curve or #sinusoid is a wave form whose function belongs to a family of functions known as #transcendentalFunctions that also include #logarithmic and #exponential functions. I mentioned #logarithmicSpirals in https://pixelfed.social/p/Splines/792499765146596723, and in a future post I will show how to construct one and compare it with the #spiral used in our implementation of #IonicVolute.

They are called transcendental functions because they transcend the math of finite algebraic polynomials and go beyond geometry into trigonometry. Fortunately, we don't have to go there.

Few #CAD tools have a direct primitive for a sinusoid, but almost all have a primitive for a 3-dimensional round coil shape called a #helix which we can use to create the sinusoids we need for a braid strand. To create a sinusoid, all we need to do is #project a helix on a flat surface to convert it into a 2D waveform.

From #PrimaryCurves to #SecondaryCurves for classic #IonicScroll

There's a lot to unpack in this diagram. For orientation, first note the 5 rectangles labeled M, N, P, Q, and R that we saw in https://pixelfed.social/p/Splines/792966507797633558, shown here in green.

The 6 blue curves are the primary curves we extracted from #imageScans in https://pixelfed.social/p/Splines/793169876757012827 and https://pixelfed.social/p/Splines/793215298082967733. The front ends of these blue primary curves are marked by points labeled F1 through F6, all of which make contact with the green rectangles of the scroll #scaffolding. The rear ends of the primary curves would be marked similarly by points R1 through R6, but they are not shown here to reduce clutter.

The orange points T1 through T5 mark where the large orange spiral is tangential to rectangles M and N. Point T6 marks the maxima for the second arm of the spiral, with the horizontal tangent shown in magenta.

In https://pixelfed.social/p/Splines/790571135473463588, I said that one way to think about #curveExtraction is to shine an imaginary bright light on an object from behind in a dark room to reveal its silhouette.

It is obvious that the blue primary curves that we extracted from image scans have NO contact with the orange spiral at any point. If you imagine shining a light on an object to #project its outline on a screen behind it, then it should also be obvious that no part of the object will be in contact with the projected outline.

So, here we are faced with the opposite problem. Instead of extracting the outlines from the #scroll, we want to recreate the scroll from the outlines that we extracted from image scans. We know the scroll exists because we can "see" its outline. Yet, like a visually-impaired person, we must "feel" our way to the scroll using the blue outlines as our #walkingStick.

Next, I show how we can feel our way around this scene to recover the secondary curves to reconstruct the scroll surface.

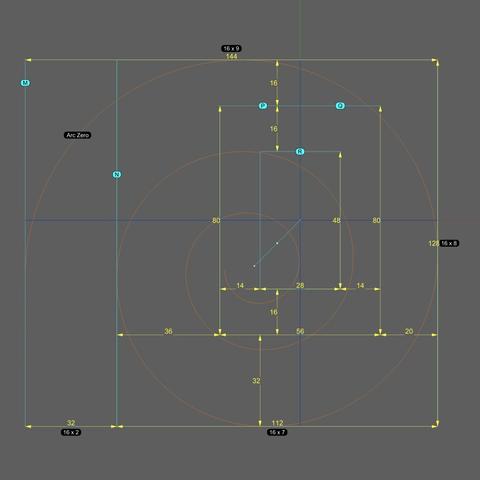
Classic #IonicScroll #Scaffolding

Take the time to understand the measurements of this scaffolding plan in the broader context of the #IonicCapital measurements, as this is the bedrock on which the #scroll reconstruction rests.

First, note that there are 5 rectangles labeled M, N, P, Q, and R, where M and N are coplanar with the large #volute at the front of the scroll. P and Q are congruent, with P exactly midway between the front and the back of the scroll, and Q exactly 3/4 of the way from front, or 1/4 from back. R is the smallest of them and lies at the back of the bell-shaped part of the scroll, but ahead of the ribbon bearing the 3-strand #braid.

M completely encloses the volute, including #ArcZero, but much of Arc zero is discarded later. So, the part of the volute that really matters is enclosed by N, whose width is 112 units, height the same as M at 128 units, and the width of M itself is exactly µ or 144 units. So these measurements are in the ratio 7:8:9.

The width of P and Q is 56 units, which is exactly half the width of N. Recall from the post on #IonicCapital #Tectonic Surfaces [https://pixelfed.social/p/Splines/792124787573855518] that the unadorned capital is also exactly 112 units, divided into two halves of 56 units each.

R is concentric with P and Q and its width is exactly half of the width of P and Q, which are exactly half the width of N.

Top of R is 32 units from top of N and 16 units from top of P and Q. Bottom of P and Q are 32 units from bottom of N and 16 units from bottom of R.

Finally note the diagonal line from the origin to the #eye with a point in the middle. That middle point is the center of rectangle labeled N. It shows that the volute #eye, the center of N and the centers of concentric rectangles P, Q, and R would be collinear if these rectangles were coplanar.

All of these constraints point to warrantable consistency and coherence of the scaffolding measurements, justifying their use in scroll reconstruction.

The classic #IonicScroll is the most complex of all components in the #IonicOrder mainly because it is poorly documented, if at all, and even poorly understood. It is as if the classical architects deliberately concealed its enigmatic design secrets within the confines of a smooth elegant shell that could only be revealed after intense study and analysis.

I got this impression because I spent years searching for credible and actionable documentation on how to recreate this beautiful design in a #CAD tool. In the Age of Internet and Social Media, my web searches always disappointed me because the results lacked something vital in one respect or another. Over the years, I created hundreds of versions of the scroll that looked so perfect and pleasing that I thought I had cracked it, only to find some flaw or another in my work.

So, it is with caution that I present my work on the scroll in the hopes that someone will build upon this knowledge and either validate the design, or correct it and share it with me and the rest of the world.

Looking back at my progress, I'm now surprised at how remarkably simple and elegant the design is that defied familiar geometrical construction techniques I had been using until now.

As I mentioned in my introductory post, this design can be recreated by drawing simple 2-dimensional lines and circular arcs, but instead of just #primaryProfileCurves, we will use up to three additional sets of curves — #secondaryCurves, #tertiaryCurves, and #quaternaryCurves — each derived from the previous set.

I extracted the #primaryCurves after a lengthy trial-and-error process that involved #curveFitting image scans from #Vignola’s book, #RegolaArchitettura. I had to #reverseEngineer the details because the measurements have either been lost, or are locked away in some library.

Even though we start with lines and arcs, the end results are always #NURBS curves and surfaces, but everything is done by the CAD tool, and no additional math is needed.

This shows macro-level measurements for the #IonicPedestal.

The key to #effectiveModeling is to simplify a complex shape into elementary components. Sometimes, this involves mentally flattening and reducing 3D shapes to 2D shapes, extracting elementary curves from them, and then recreating the 3D shapes from the extracted 2D curves.

This is not always easy for organic shapes (which can still be approximated by Bézier curves). I extracted the #primaryCurves for the #IonicScroll surface in https://pixelfed.social/p/Splines/789956327130679640 after a lengthy trial-and-error process that involved #curveFitting images from #Vignola’s book, #RegolaArchitettura. I had to #reverseEngineer the details because the measurements have either been lost, or are locked away in some library. Web search yields no details on these measurements.

Fortunately, for geometrical shapes like pedestals, this is very easy. Because of its square footprint, mentally slicing it through the middle from top to bottom, it is easy to “see” the outline. Another way to think about #curveExtraction is to shine an imaginary bright light on an object from behind in a dark room to reveal its silhouette.

For the pedestal, even this silhouette or outline can be further reduced because the shape is symmetrical about the #columnAxis. With this realization, we only need to focus on one half of the outline, and methodically proceed from bottom to top, marking every kink and inflection point on the outline.

Fortunately, the other authoritative book, #Scarlata’s #PracticalArchitecture, I mentioned in my introductory post already documents #VignolaProportions in tabular form. So we can skip everything else and go directly to that.

Total height of #IonicPedestal is 864 units (108 parts, or 6*µ) of which the #PedestalBasement and #PedestalCap are each 72 units (9 parts, or µ/2) and the #Dado is 720 units (90 parts, or µ*5) tall.

Front view of the wireframe with some sections and the zebra pattern removed to reveal the complexity of the surface of the #IonicScroll. This helps us "see" complex 3-dimensional shapes as flat 2-dimensional curves that can be manipulated in a CAD tool to bring them into the 3rd dimension.

As mentioned in https://pixelfed.social/p/Splines/789956327130679640, this design can be recreated exclusively by drawing simple 2-dimensional straight lines and circular arcs snapped to grid points using specific measurements.

The nearly circular edge on the outside is towards the front of the #scroll and the nearly oval edge in the middle is towards the back of the scroll in 3D space. I say "nearly" because neither is a perfect circle or ellipse. The outer one is created with sections of perfectly circular arcs and the inner one by nonuniform scaling of the outer one — exactly 1/4 in the X direction and 3/8 in the Y direction.

I will show the reconstruction methodology and exact measurements for every detail using 2D vector shapes without being burdened by the user interface of any specific CAD tool.

The measurements are critical, as changing any of them will change the appearance and destroy the coherence of the entire order. That does not mean there's no opportunity for alternative creative expression. Far from it. The design methodology I present separates the #tectonic elements of a design from the #decorative elements.

So, anyone can enhance the designs with custom art, whether with 3D vector inlays, overlays, carvings, and so on, or with pixel art using paintbrushes and textures on the tectonic surfaces. With some imagination, one can even repurpose basic shapes and surfaces, or portions thereof, into completely different designs such as model trains and fashion accessories.

The idea is to create a design platform that designers worldwide could contribute to or use in their own private projects while maintaining interoperability to foster sharing or commerce.

#IonicScroll

Client Info